Introduction
On s'intéresse à une réaction de type A \(\rightarrow\) produits catalysée par un solide. Le réactif A est fluide, ainsi que les produits de réaction.
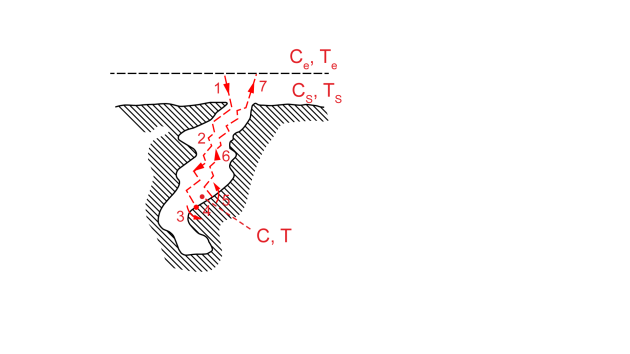
Comme illustré sur la figure suivante, on distingue habituellement 7 étapes pour réaliser une réaction catalytique :
l'espèce(s) réactive(s) présente(s) dans la phase fluide vien(nen)t en surface du grain de catalyseur (phénomène de transfert externe) ;
l'espèce(s) réactive(s) présente(s) dans la phase fluide migre(nt) à l'intérieur d'un pore du grain de catalyseur par diffusion ;
l'espèce(s) réactive(s) présente(s) dans la phase fluide s'adsorbe(nt) sur un site actif de catalyseur ;
la réaction a lieu ;
les produits de réaction non solide désorbent ;
les produits de réaction migrent vers l'extérieur du catalyseur via un pore du grain de catalyseur par diffusion ;
les produits de réaction s'éloignent du grain de catalyseur (phénomène de transfert externe).
Selon la réaction étudiée et selon la configuration du catalyseur utilisé, certaines de ces étapes sont rapides, d'autres plus lentes. La vitesse globale de la réaction sera la combinaison des vitesses de toutes ces étapes. En particulier si l'une des étapes est très lente, sa vitesse s'imposera à l'ensemble du processus ; on la qualifiera alors d'étape limitante.
Généralement on rassemble les cinétiques d'adsorption/désorption et la loi de vitesse de la réaction au sein d'une même expression, qui a typiquement (dans les cas les plus simples) la forme suivante :
\(\overline{r} = \frac{k_1 \cdot C_A}{1 + k_2 \cdot C_A}\) et parfois \(\overset{\_}{r} = \frac{k_1 \cdot C_A}{1 + k_2 \cdot C_A + k_3 \cdot C_P}\)
où \(A\) est le réactif et \(P\) le produit de la réaction ; \(\overline{r}\) est la vitesse moyenne rapportée à l'unité de volume du catalyseur.
Cependant sur un intervalle de concentration limité, cette expression peut se ramener à \(\overline{r} = k \cdot {C_A}^n\), où \(k\) ne suit généralement plus une loi d'ARRHÉNIUS pour la dépendance en température.
Dans un certain nombre de démonstrations qui vont suivre, nous nous limiterons au premier ordre (\(n = 1\)).