Notions de rhéologie
Les fluides peuvent avoir des comportements très hétéroclites. Il s'agit ici simplement de mentionner ces comportements ; ce n'est nullement un cours de rhéologie.
Notion fondamentale :
Pour classifier les fluides, on se base généralement sur l'expression suivante, qui relie la contrainte \(\tau\) (force par unité de surface) à la déformation \(\overset{\bullet }{\mathop{\gamma }} = \frac{du}{dz}\) que cette contrainte occasionne :
Définition :
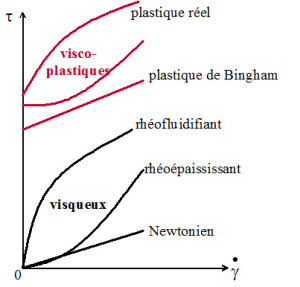
Dans le cas des fluides parfaits, c'est-à-dire sans frottements, la viscosité dynamique est nulle. Pour les fluides réels (c'est-à-dire non-parfaits), on distingue plusieurs cas :
les fluides Newtonien, pour lesquels la viscosité dynamique est constante ;
les fluides non-Newtonien dont le comportement est indépendants du temps, qui peuvent être visqueux (sans contrainte seuil) ou plastiques (avec contrainte seuil, c'est-à-dire qu'il faut leur appliquer une contrainte minimale pour réussir à les mettre en mouvement) ;
les fluides thixotropes, dont le comportement est dépendant du temps.
Remarque : Lois rhéologiques
Les lois rhéologiques les plus usuelles sont les suivantes :
loi d'Oswald : \(\tau ={{\mu }_{0}}\cdot {{\left( \overset{\bullet }{\mathop{\gamma }}\, \right)}^{n}}\)
loi de Bingham : \(\tau ={{\tau }_{0}}+{{\mu }_{B}}\cdot \overset{\bullet }{\mathop{\gamma }}\,\)
loi d'Hershell-Bulkley : \(\tau ={{\tau }_{0}}+{{K}_{B}}\cdot {{\left( \overset{\bullet }{\mathop{\gamma }}\, \right)}^{{{n}_{B}}}}\)
loi de Casson : \(\sqrt{\tau }=\sqrt{{{\tau }_{0}}}+\sqrt{{{\mu }_{C}}\cdot \overset{\bullet }{\mathop{\gamma }}\,}\)