Dimensionnement d'une pompe centrifuge alimentant un décanteur depuis un cristalliseur
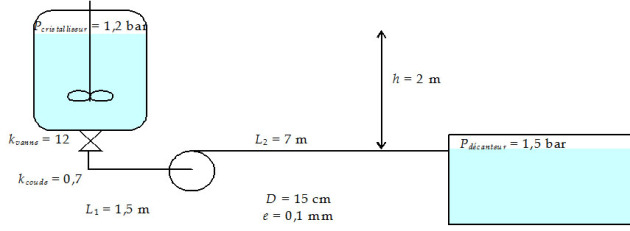
Un décanteur est alimenté depuis un cristalliseur via une pompe centrifuge. Le niveau (constant) de solvant dans le cristalliseur est 2 m au-dessus de celui dans le décanteur (également à niveau constant). La pression dans le ciel du cristalliseur est de 1,2 bar. Pour un bon fonctionnement du décanteur, la pression à son entrée doit être de 1,5 bar.
La canalisation entre le cristalliseur et la pompe mesure 1,5 m de long et a un diamètre interne 15 cm. Elle est en acier, de rugosité 0,1 mm. Elle comporte une vanne de fond de cuve (dont le coefficient de perte de charge vaut 12) et un coude arrondi (dont le coefficient de perte de charge vaut 0,7).
La canalisation entre la pompe et le décanteur est identique à celle côté aspiration, mais mesure 7 m de long. Elle ne comporte pas de singularité.
La pompe a un rendement de 57%.
On assimile les propriétés de la suspension produite par le cristalliseur à celles du solvant, soit une masse volumique de 875 kg m-3 et une viscosité de 5 10-3 Pa s.
Question
Calculer la hauteur manométrique totale (en mètre de colonne d'eau) et la puissance de la pompe nécessaire.
Indice
Commencez par faire un schéma de l'installation et portez-y les différentes données de l'énoncé.
Indice
Écrire l'équation de Bernouilli généralisée entre la surface (immobile) du liquide dans le cristalliseur et l'entrée dans le décanteur.
Puis évaluer les pertes de charge régulières et singulières sur l'ensemble du circuit entre le cristalliseur et le décanteur.
En déduire la hauteur manométrique totale puis la puissance de la pompe nécessaire.
Solution détaillée
On écrit l'équation de Bernouilli généralisée entre la surface (immobile) du liquide dans le cristalliseur et l'entrée dans le décanteur :
\({{P}_{crist}}+\rho \cdot g\cdot {{z}_{crist}}+\frac{\rho \cdot 0^2}{2} + \Delta P_{pompe}={{P}_{decant}}+\rho \cdot g\cdot {{z}_{decant}}+\frac{\rho \cdot {{u}_{decant}}^{2}}{2} + \Delta P_{f}\)
avec \(\Delta {{P}_{f}}=\Delta {{P}_{fr}}+\sum{\Delta {{P}_{fs}}}=\frac{\rho \cdot {u^2}}{2}\cdot \left( \frac{8\cdot {}^{f}/{}_{2}\cdot \left( L_{1} +L_{2} \right)}{D} +k_{vanne} +k_{coude} \right)\)
On calcule la vitesse \(u = \frac{4 \cdot Q_{v}}{\pi \cdot D^2}=\frac{4 \cdot \frac{300}{3600}}{\pi \cdot 0,15^2} =\) 4,716 m s-1
On en déduit le nombre de Reynolds \(Re = \frac{ \rho \cdot u \cdot D}{\mu} = \frac{ 875 \cdot 4,716 ^ 0,15}{5 \cdot 10^-3} =\) 123 787
On calcule également la rugosité relative \(\frac{e}{R} = \frac{0,1}{75} =\) 0,0013
On peut alors placer le point correspondant sur le diagramme de Moody :
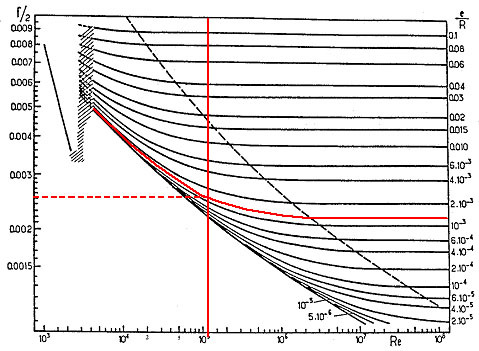
On en déduit que le régime est intermédiaire et que le facteur de frottement vaut environ 0,0025.
La relation de Churchill fournit une valeur plus précise :
\({f}/{}_{2}={\left( 2,457\cdot \ln \ {{\left[ {{\left( \frac{7}{Re} \right)}^{0,9}}+0,27\cdot \frac{e}{D} \right]}^{-1}} \right)}^{-2}=\) 0,00258
Finalement \(\Delta P_{pompe}={{P}_{decant}} - {{P}_{crist}} -\rho \cdot g\cdot h +\frac{\rho \cdot {u}^{2}}{2} \cdot \left(1 +\frac{8\cdot {}^{f}/{}_{2}\cdot \left( L_{1} +L_{2} \right)}{D} +k_{vanne} +k_{coude} \right)\)
\({{P}_{decant}} - {{P}_{crist}} =\) 30 000 Pa : variation de pression statique
\(-\rho \cdot g\cdot h =\) -17 168 Pa : variation d'énergie potentielle (par unité de volume)
\(\frac{\rho \cdot {u}^{2}}{2}=\) 9 729 Pa : variation d'énergie cinétique (par unité de volume)
\(\frac{\rho \cdot {u}^{2}}{2} \cdot \frac{8\cdot {}^{f}/{}_{2}\cdot \left( L_{1} +L_{2} \right)}{D} =\) 11 372 Pa : pertes de charge régulières
\(\frac{\rho \cdot {u}^{2}}{2} \cdot \left(k_{vanne} +k_{coude} \right) =\) 123 559 Pa : pertes de charge singulières
Soit au total \(\Delta P_{pompe}=\) 157 493 Pa
D'où \(H_{mt}=\frac{\Delta P_{pompe}}{\rho_{eau} \cdot g}=\) 16,1 mCE
Enfin \(\mathcal{P}_{elect} = \frac{Q_{v} \cdot \Delta{P_{pompe}}}{\eta}=\) 23 kW, ce qui n'est pas rien !