Répartition de débits
Un circuit d'huile est composé de deux conduites parallèles : la première de 200 m de longueur et de 100 mm de diamètre ; la seconde de 250 m de longueur et de 150 mm de diamètre. Le débit total est de 25 L/s. La masse volumique de l'huile est de 1000 kg m-3 et sa viscosité de 10-1 Pa s.
On supposera que le régime est laminaire dans tout le circuit, et on vérifiera cette hypothèse a posteriori.
Question
Calculer les débits dans les deux conduites.
Indice
Écrire la conservation du débit total d'une part et l'égalité des pertes de charge dans chacune des deux branches d'autre part. Ceci fournira deux équations dont les inconnues sont les débits dans les deux conduites.
Indice
Ne pas oublier de calculer ensuite les nombres de Reynolds dans chaque branche pour vérifier l'hypothèse du régime laminaire.
Solution détaillée
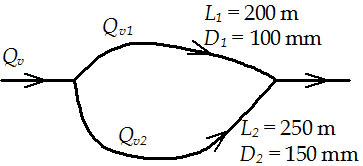
Les conduites étant parallèles, on a \(Q_{v}=Q_{v1}+Q_{v2}\) et \(\Delta {{P}_{1}}=\Delta {{P}_{2}}\).
Comme les points d'entrée et de sortie sur les deux branches sont identiques, on a en fait \(\Delta {{P}_{f1}}=\Delta {{P}_{f2}}\).
Si on fait l'hypothèse d'un régime laminaire dans chaque branche, \(\Delta {{P}_{f1}}=32\cdot \frac{\mu \cdot \overline{u_{1}}\cdot L_{1}}{{{D_{1}}^{2}}}\) et \(\Delta {{P}_{f2}}=32\cdot \frac{\mu \cdot \overline{u_{2}}\cdot L_{2}}{{{D_{2}}^{2}}}\).
Donc \(\frac{Q_{v1}\cdot L_{1}}{\frac{\pi \cdot {{D_{2}}^{2}}}{4} \cdot{{D_{1}}^{2}}}=\frac{Q_{v2}\cdot L_{2}}{ \frac{\pi \cdot {{D_{2}}^{2}}}{4} \cdot {{D_{2}}^{2}}}\), soit \(\frac{Q_{v1} \cdot L_{1}}{{D_{1}}^{4}}=\frac{Q_{v2} \cdot L_{2}}{{D_{2}}^{4}}\).
Par conséquent \(\left\{ \begin{array}{r l}& Q_{v}=Q_{v1}+Q_{v2} \\& \frac{Q_{v1} \cdot L_{1}}{{{D_{1}}^{4}}}=\frac{Q_{v2} \cdot L_{2}}{{{D_{2}}^{4}}} \\\end{array} \right.\).
Ainsi \(Q_{v2} = \frac{L_{1}}{L_{2}} \cdot {\left( \frac{D_{2}}{D_{1}} \right)}^{4} \cdot Q_{v1}\) et \(Q_{v} = \left( 1 + \frac{L_{1}}{L_{2}} \cdot {\left( \frac{D_{2}}{D_{1}} \right)}^{4} \right) \cdot Q_{v1}\).
D'où \(Q_{v1} = \frac{ Q_{v} }{ 1 + \frac{L_{1}}{L_{2}} \cdot {\left( \frac{D_{2}}{D_{1}} \right)}^{4} } =\) 5 L/s
Et \(Q_{v2} = Q_{v} - Q_{v1} =\) 20 L/s
On vérifie dans chaque branche :
\(Re_{1} = \frac{ \rho \cdot \frac{Q_{v1}}{ \frac{\pi \cdot {{D_{1}}^{2}}}{4} } \cdot D_{1} }{ \mu } = \frac{ 4 \cdot \rho \cdot Q_{v1} }{ \pi \cdot \nu \cdot D_{1}} =\) 640
\(Re_{2} = \frac{ 4 \cdot \rho \cdot Q_{v2} }{ \pi \cdot \mu \cdot D_{2}} =\) 1700
Le régime est bien laminaire dans chacune des branches.