Fabrication d'huiles siccatives à partir d'huile de ricin
L'huile de ricin, constituée essentiellement par un glycéride de l'acide ricinoléique, peut être acétylée. Par perte d'une molécule d'acide acétique, on obtient de l'huile de ricin déshydratée constituée par des glycérides d'acides linoléiques qui sont des acides diéniques conjugués doués de propriétés siccatives.
La réaction s'écrit : huile de ricin acétylée → acide acétique + huile siccative
Cette réaction est d'ordre 1 par rapport à l'huile de ricin acétylée, dont la concentration est exprimée en gramme d'acide acétique libérable par cm3 d'huile. La constante de vitesse, exprimée en min-1, est donnée, entre 300 et 600°C, par : \(k=\exp \ \left( 35,2 - \frac{44500}{R \cdot T} \right)\), avec \(T\) en K et \(R =\) 1,9865 cal mol-1 K-1
La concentration initiale est égale à 0,156 g d'acide acétique libérable par gramme d'huile, dont la masse volumique est de 0,9 g/cm3.
Question
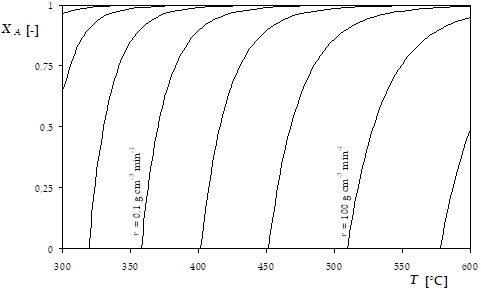
Exprimer le taux de conversion d'huile \(X_A\) en fonction de la vitesse de réaction \(r\) et de la température \(T\). Tracer \(X_A\) vs \(T\) pour diverses valeurs de \(r\).
Solution
\(r = k \cdot C_A\) (\(C_A\) est la concentration en huile de ricin acétylée, exprimée en gramme d'acide acétique libérable par cm3 d'huile). En phase liquide, on considérera que le volume est constant et \(C_A = C_{A0} \cdot (1 - X_A)\)
D'où \(X_A = 1 - \frac{r}{0,156 \cdot 0,9 \cdot \exp \ \left( 35,2 - \frac{44500}{1,9865 \cdot T} \right)}\), avec \(r\) en g d'ac. ac. libérable par cm3 d'huile et \(T\) en K.
La réaction est endothermique, avec \(\Delta r H =\)15 kcal mol-1 dans la même gamme de températures. La capacité calorifique du milieu réactionnel vaut 40 cal mol-1 K-1.
Question
Quelle conversion fournira un RPA fonctionnant en continu et adiabatique, avec un temps de passage de 1 min et pour une alimentation à 550°C ?
Solution
363°C et 49% de conversion
Solution
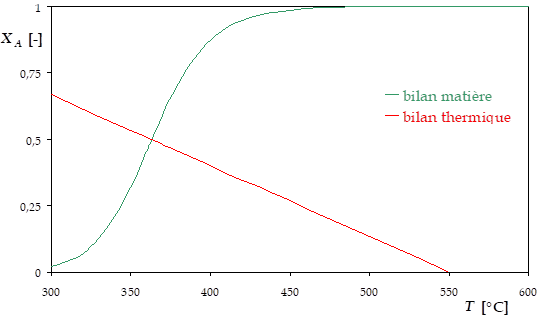
bilan matière
Le bilan matière (en huile de ricin acétylée) sur le RPA s'écrit : \(F_{A0} - r \cdot V = F_A\)
Ou encore \(C_{A0} - r \cdot \tau = C_{A0} \cdot \left( 1 - X_A \right)\)
Soit \(r \cdot \tau = C_{A0} \cdot X_A = k \cdot C_{A0} \cdot \left( 1 - X_A \right) \cdot \tau\), donc \(X_A = \frac{k \cdot \tau}{1 + k \cdot \tau}\)
D'où \(X_A = \frac{\exp \ \left( 35,2 - \frac{44500}{1,9865 \cdot T} \right) \cdot 1}{1 + \exp \ \left( 35,2 - \frac{44500}{1,9865 \cdot T} \right) \cdot 1}\), avec \(T\) en K
bilan thermique
Le bilan thermique en marche adiabatique s'écrit : \(0 = F \cdot Cp \cdot \left( T^s - T^e \right) + F_{A0} \cdot X_A \cdot \Delta rH\) (\(Cp\) molaire)
où \(F \cdot Cp = F_{A0} \cdot Cp\), d'où \(\frac{T^s - T^e}{X_A} = -\frac{\Delta rH}{Cp}\), soit \(X_A = \frac{Cp}{\Delta rH} \cdot \left( T^e - T^s \right)\)
D'où \(X_A = \frac{0,04}{15} \cdot \left( 550 - T^s \right)\), avec \(T\) en K
bilans couplés

L'intersection de la courbe représentant le bilan matière et de la droite représentant le bilan thermique donne le point de fonctionnement du RPA : 363°C et 49% de conversion.
Question
Reprise de toutes les questions en vidéo.
Solution
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.