Réaction exothermique renversable
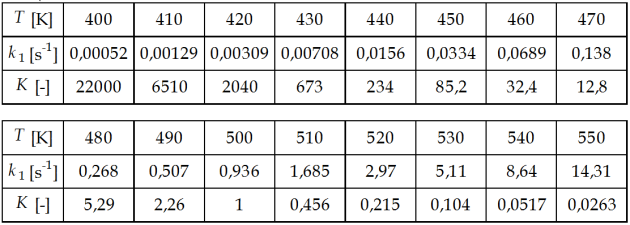
On considère la réaction en phase liquide A ⇄ B . Elle est du premier ordre par rapport au réactif dans les deux sens. Une étude préalable de la cinétique et de la thermodynamique de cette réaction a donné les résultats suivants (où \(k_1\) est la constante de vitesse de réaction dans le sens direct, \(k_2\) est la constante de vitesse de réaction dans le sens indirect et \(K\) est la constante d'équilibre) :
Question
Déterminer l'enthalpie de réaction \(\Delta r H\) ainsi que les énergies d'activation \(Ea_1\) et \(Ea_2\).
Solution
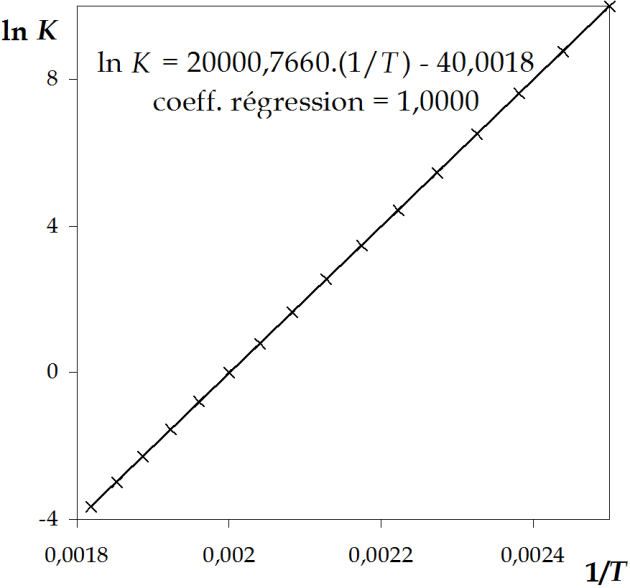
\(- \Delta r H\) n'est autre que la pente de la droite \(\ln K \: vs \: \frac{1}{T}\), soit \(\Delta r H =\) -166,3 kJ mol-1
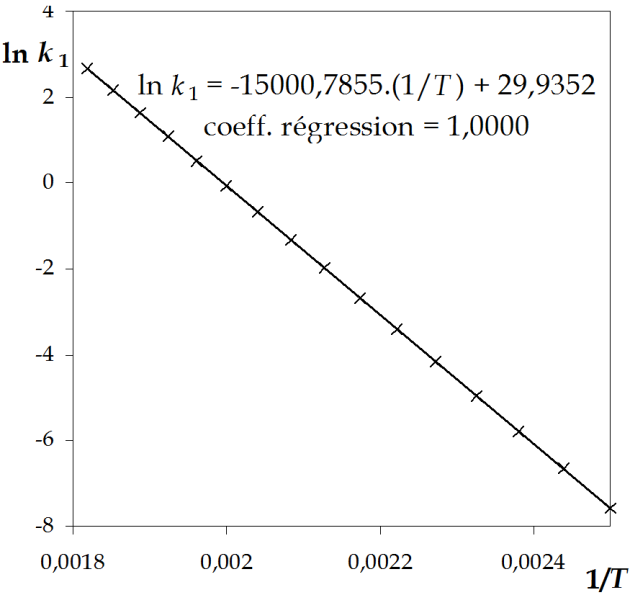
\(- \frac{Ea_1}{R}\) n'est autre que la pente de la droite \(\ln k_1 \: vs \: \frac{1}{T}\), soit \(Ea_1 =\) 124,7 kJ mol-1
\(K = \frac{k_1}{k_2}\), donc \(\Delta r H = Ea_1 - Ea_2\), d'où \(Ea_2 =\) 291,0 kJ mol-1
Solution
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Question
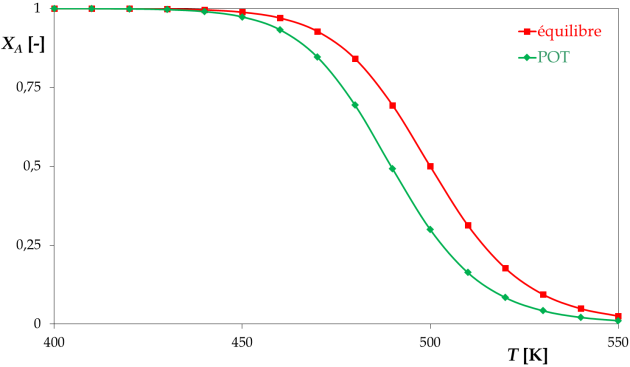
Calculer le taux de conversion à l'équilibre, ainsi que celui correspondant à la P.O.T., en fonction de la température.
Solution
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Solution
équilibre
En phase liquide, on considérera que le volume est constant : \(C_A = C_{A0} \cdot (1 - X_A)\) et \(C_B = C_{A0} \cdot X_A\). (On suppose que l'alimentation du réacteur ne contient pas de B.)
\(K = \frac{a_B^{eq}}{a_A^{eq}} \approx \frac{C_B^{eq}/C^0}{C_A^{eq}/C^0} = \frac{C_B^{eq}}{C_A^{eq}} = \frac{C_{A0} \cdot X_A^{eq}}{C_{A0} \cdot \left( 1 - X_A^{eq} \right)} = \frac{X_A^{eq}}{1 - X_A^{eq}}\), donc \(X_A^{eq} \approx \frac{K}{1+K}\)
P.O.T.
La POT correspond à \(\frac{\partial r}{\partial T} = 0\).
Or \(r = k_1 \cdot C_A - k_2 \cdot C_B = C_{A0} \cdot \left[ k_1 \cdot \left( 1 - X_A \right) - k_2 \cdot X_A \right]\)
Soit \(r = C_{A0} \cdot \left[ k_{0,1} \cdot \exp \ \left( \frac{-Ea_1}{R \cdot T} \right) \cdot \left( 1 - X_A \right) - k_{0,2} \cdot \exp \ \left( \frac{-Ea_2}{R \cdot T} \right) \cdot X_A \right]\)
Donc \(\frac{\partial r}{\partial T} = C_{A0} \cdot \left[ \frac{Ea_1}{R \cdot T^2} \cdot k_{0,1} \cdot \exp \ \left( \frac{-Ea_1}{R \cdot T} \right) \cdot \left( 1 - X_A \right) - \frac{Ea_2}{R \cdot T^2} \cdot k_{0,2} \cdot \exp \ \left( \frac{-Ea_2}{R \cdot T} \right) \cdot X_A \right]\)
Cette dérivée s'annule sur la P.O.T., soit \(C_{A0} \cdot \left[ \frac{Ea_1}{R \cdot T^2} \cdot k_1 \cdot \left( 1 - X_A^{POT} \right) - \frac{Ea_2}{R \cdot T^2} \cdot k_2 \cdot X_A^{POT} \right] = 0\)
D'où \(X_A^{POT} = \frac{Ea_1 \cdot k_1}{Ea_1 \cdot k_1 + Ea_2 \cdot k_2} = \frac{1}{1+\frac{Ea_2 \cdot k_2}{Ea_1 \cdot k_1}} = \frac{1}{1 +\frac{Ea_2}{Ea_1 \cdot K}}\)
Question
Pour une alimentation comprenant uniquement l'espèce A, calculer le taux de conversion en sortie d'un réacteur piston isotherme (de temps de passage 20 s) en fonction de la température de réaction. Tracer la courbe correspondante et déterminer la température optimale et l'avancement correspondant. Ce point est-il sur la P.O.T. ?
Quelle serait la conversion optimale (pour le même temps de passage) dans un réacteur parfaitement agité lui-aussi isotherme ? Ce point est-il sur la P.O.T. ?
Quel flux de chaleur faut-il évacuer pour assurer ce fonctionnement optimal dans un RPA isotherme alimenté par 100 mol min-1 de réactif A à la température de 300 K ; la capacité calorifique du milieu étant de 50 J mol-1 K-1 ?
Enfin, comment faire pour obtenir un taux de conversion de 95% ? (expliquer qualitativement)
Solution
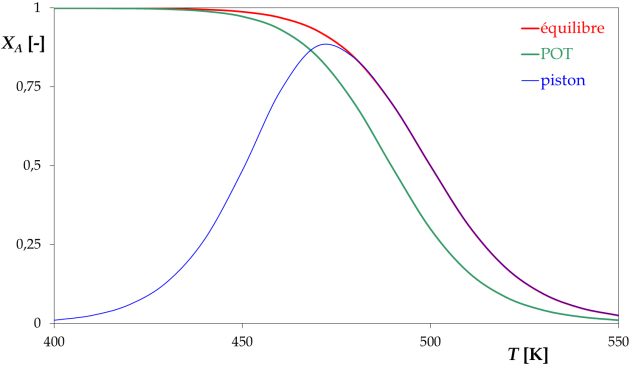
réacteur piston
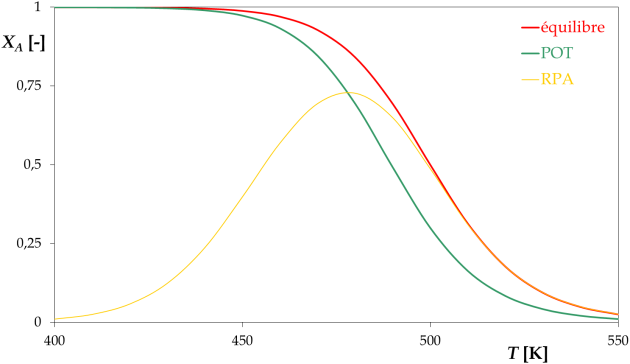
RPA
flux de chaleur à évacuer du RPA
186,5 kW
Conseil : 95 % de conversion
Pour pouvoir atteindre un taux de conversion de 95%, il faudra prévoir plusieurs réacteurs successifs, avec des refroidisseurs intermédiaires, afin de suivre un chemin "autour" de la P.O.T.
Solution
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Solution
réacteur piston
Le bilan en A sur le réacteur piston s'écrit : \(\mathrm{d}F_A = - r \cdot \mathrm{d}V\)
Soit \(-F_{A0} \cdot \mathrm{d}X_A = -\left[ k_1 \cdot C_{A0} \cdot \left( 1 - X_A \right) - k_2 \cdot C_{A0} \cdot X_A \right] \cdot \mathrm{d}V = -C_{A0} \cdot k_1 \cdot \left( 1 - X_A - \frac{X_A}{K} \right) \cdot \mathrm{d}V\)
Donc \(C_{A0} \cdot Q_v \cdot \mathrm{d}X_A = C_{A0} \cdot k_1 \cdot \left( 1 - X_A - \frac{X_A}{K} \right) \cdot \mathrm{d}V\)
D'où \(\mathrm{d}X_A = k_1 \cdot \left( 1 - X_A - \frac{X_A}{K} \right) \cdot \frac{\mathrm{d}V}{Q_v} = k_1 \cdot \left( 1 - X_A -\frac{X_A}{K} \right) \cdot \mathrm{d}\tau\)
Ou encore \(\frac{\mathrm{d}X_A}{1 - X_A - \frac{X_A}{K}} = \frac{-1}{1 + \frac{1}{K}} \cdot \frac{\mathrm{d} \left( 1 - X_A - \frac{X_A}{K} \right)}{1 - X_A -\frac{X_A}{K}} = k_1 \cdot \mathrm{d}\tau\)
Après intégration, \(\ln \ \left( 1 - X_A^{piston} - \frac{X_A^{piston}}{K} \right) = -k_1 \cdot \left( 1 + \frac{1}{K} \right) \cdot \tau\) ; soit \(X_A^{piston} = \frac{1 - \exp \ \left[ -k_1 \cdot \left( 1 + \frac{1}{K} \right) \cdot \tau \right]}{1 + \frac{1}{K}}\)
Finalement \(X_A^{piston} = X_A^{eq} \cdot \left[ 1 - \exp \ \left( - \frac{k_1 \cdot \tau}{X_A^{eq}} \right) \right]\)
L'optimum correspond à une température de 470 K, le taux de conversion vaut alors 88,0%.
Ce point n'a aucune raison de se trouver sur la POT.
RPA
Le bilan en A sur le RPA s'écrit : \(F_{A0} - r \cdot V = F_A\)
Soit \(F_{A0} - \left[ k_1 \cdot C_{A0} \cdot \left( 1 - X_A^{RPA} \right) - k_2 \cdot C_{A0} \cdot X_A^{RPA} \right] \cdot V = F_{A0} \cdot \left( 1 - X_A^{RPA} \right)\)
Ou encore \(-\left[ k_1 \cdot C_{A0} \cdot \left( 1 - X_A^{RPA} \right) - k_2 \cdot C_{A0} \cdot X_A^{RPA} \right] \cdot V = -F_{A0} \cdot X_A^{RPA} = -C_{A0} \cdot Q_v \cdot X_A^{RPA}\)
Donc \(\left[ k_1 \cdot \left( 1 - X_A^{RPA} \right) - k_2 \cdot X_A^{RPA} \right] \cdot \tau = X_A^{RPA}\)
D'où \(X_A^{RPA} = \frac{k_1 \cdot \tau}{1 + k_1 \cdot \tau + k_2 \cdot \tau} = \frac{k_1 \cdot \tau}{1 + k_1 \cdot \tau \cdot \left( 1 + \frac{1}{K} \right)}\), soit \(X_A^{RPA} = \frac{k_1 \cdot \tau}{1 + \frac{k_1 \cdot \tau}{X_{eq}}}\)
L'optimum correspond à une température de 480 K, le taux de conversion vaut alors 72,7%.
Ce point se trouve sur la POT, car dans un RPA la vitesse est la même partout.
bilan thermique sur le RPA
Le bilan thermique s'écrit : \(\phi = F_{A0} \cdot Cp \cdot \left( T^s - T^e \right) + F_{A0} \cdot X_A^s \cdot \Delta rH\)
L'application numérique donne 186,5 kW à évacuer.
Conseil : 95 % de conversion
Pour pouvoir atteindre un taux de conversion de 95%, il faudra prévoir plusieurs réacteurs successifs, avec des refroidisseurs intermédiaires, afin de suivre un chemin "autour" de la P.O.T.