Génie de la Réaction Chimique : les réacteurs homogènes

\(\eta'_{R/A} = \frac{k_1}{k_1 + 2 \cdot k_2 \cdot C_{A0} \cdot \left( 1 - X_A \right)}\)

Puisque l'on travaille en phase liquide, et sans autre précision, on suppose que le volume réactionnel ne varie pas. Ainsi \(C_A = C_{A0} \cdot \left( 1 - X_A \right)\).

Le rendement relatif du produit R par rapport au réactif A est : \(\eta'_{R/A} = \frac{\mathbb{R}_R}{\nu_{R/A} \cdot \left( - \mathbb{R}_A \right) } = \frac{r_1}{r_1 + 2 \cdot r_2}\)

Soit : \(\eta'_{R/A} = \frac{k_1 \cdot C_A}{k_1 \cdot C_A + 2 \cdot k_2 \cdot C_A^2} =\frac{k_1}{k_1 + 2 \cdot k_2 \cdot C_A}\). D'où \(\eta'_{R/A} = \frac{k_1}{k_1 + 2 \cdot k_2 \cdot C_{A0} \cdot \left( 1 - X_A \right)}\)

RPA ; \(X_A^s =\) 1 ; mais alors le volume du réacteur est infini

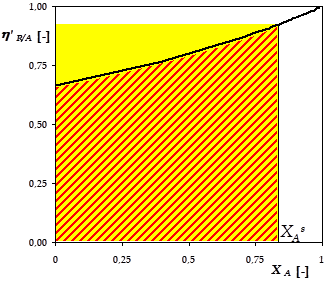
\(\eta'_{R/A}\) étant une fonction croissante de \(X_A\), \(Y_{R/A}\) sera maximum dans un RPA (aire en jaune) par rapport à un réacteur piston (aire hachurée de rouge) :

\(\eta'_{R/A}\) est de surcroît maximum pour \(X_A^s =\) 1

Le bilan en A dans un RPA s'écrit : \(F_A^e + \left( - r_1 - 2 \cdot r_2 \right) \cdot V_{RPA} = F_A^s\)

Soit :

\(F_{A0} - \left[ k_1 \cdot C_{A0} \cdot \left( 1 - X_A^s \right) + 2 \cdot k_2 \cdot C_{A0}^2 \cdot \left( 1 - X_A^s \right)^2 \right] \cdot V_{RPA} = F_{A0} \cdot \left( 1 - X_A^s \right)\)

Soit \(F_{A0} \cdot X_A^s = \left[ k_1 \cdot C_{A0} \cdot \left( 1 - X_A^s \right) + 2 \cdot k_2 \cdot C_{A0}^2 \cdot \left( 1 - X_A^s \right)^2 \right] \cdot V_{RPA}\)

D'où \(V_{RPA} = \frac{F_{A0} \cdot X_A^s}{k_1 \cdot C_{A0} \cdot \left( 1 - X_A^s \right) + 2 \cdot k_2 \cdot C_{A0}^2 \cdot \left( 1 - X_A^s \right)^2}\), qui tend vers l'infini quand \(X_A^s\) tend vers 1.

coût minimum pour un taux de conversion de A en sortie de 79,48% ; alors \(\mathcal{P}_R =\) 0,2812 € mol^-1

En observant attentivement les unités, on peut établir le bilan économique : \(\mathcal{P}_R \cdot F_R^s = \mathcal{P}_A \cdot F_{A0} + \mathcal{P}'_{fonctionnement} \cdot V_{RPA}\), soit \(\mathcal{P}_R = \mathcal{P}_A \cdot \frac{F_{A0}}{F_R^s} + \mathcal{P}'_{fonctionnement} \cdot \frac{V_{RPA}}{F_R^s}\)

D'une part, \(Y_{R/A} = \frac{F_R^s}{1 \cdot F_{A0}}\), donc \(\mathcal{P}_R = \frac{\mathcal{P}_A}{Y_{R/A}} + \frac{\mathcal{P}'_{fonctionnement} \cdot V_{RPA}}{F_{A0} \cdot Y_{R/A}}\)

Or \(Y_{R/A} = \int\limits_{0}^{X_A^s}{\eta'_{R/A} \left( X_A \right) \cdot \mathrm{d}X_A}\) (l'écriture \(\eta'_{R/A} \left( X_A \right)\) signifie ici : la valeur de \(\eta'_{R/A}\) en \(X_A\), car il n'y a pas de signe de multiplication entre \(\eta'_{R/A}\) et la parenthèse). Or dans un RPA, \(\eta '_{R/A} \left( X_A \right) =\eta'_{R/A} \left( X_A^s \right) =\) constante.

Donc \(Y_{R/A} = \eta'_{R/A} \left( X_A^s \right) \cdot \int\limits_{0}^{X_A^s}{\mathrm{d}X_A} = \frac{k_1}{k_1 + 2 \cdot k_2 \cdot C_{A0} \cdot \left( 1 - X_A^s \right)} \cdot X_A^s\)

D'autre part \(V_{RPA} = \frac{F_{A0} \cdot X_A^s}{k_1 \cdot C_{A0} \cdot \left( 1 - X_A^s \right) + 2 \cdot k_2 \cdot C_{A0}^2 \cdot \left( 1 - X_A^s \right)^2} = \frac{F_{A0} \cdot X_A^s}{C_{A0} \cdot \left( 1 - X_A^s \right)} \cdot \frac{1}{k_1 +2\ cdot k_2 \cdot C_{A0} \cdot \left( 1 - X_A^s \right)}\)

D'où \(\mathcal{P}_R = \frac{\mathcal{P}_A}{\frac{k_1 \cdot X_A^s}{k_1 + 2 \cdot k_2 \cdot C_{A0} \cdot \left( 1 - X_A^s \right)}} + \frac{\mathcal{P}'_{fonctionnement} \cdot \frac{F_{A0} \cdot X_A^s}{C_{A0} \cdot \left( 1 - X_A^s \right)} \cdot \frac{1}{k_1 + 2 \cdot k_2 \cdot C_{A0} \cdot \left( 1 - X_A^s \right)}}{F_{A0} \cdot \frac{k_1 \cdot X_A^s}{k_1 + 2 \cdot k_2 \cdot C_{A0} \cdot \left( 1 - X_A^s \right)}}\)

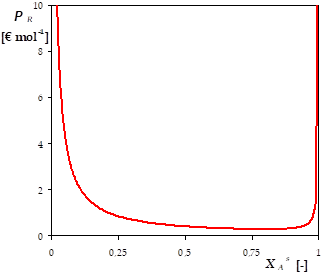
Finalement \(\mathcal{P}_R = \frac{\mathcal{P}_A \cdot \left[ k_1 + 2 \cdot k_2 \cdot C_{A0} \cdot \left( 1 - X_A^s \right) \right]}{k_1 \cdot X_A^s} + \frac{\mathcal{P}'_{fonctionnement}}{k_1 \cdot C_{A0} \cdot \left( 1 - X_A^s \right)}\). Cette fonction est représentée sur le graphique suivant.

Ainsi \(\mathcal{P}_R\) est élevé pour \(X_A^s\) faible, car on produit peu de P ; \(\mathcal{P}_R\) est également élevé pour \(X_A^s\) très élevé, car le volume du réacteur devient énorme (comme on l'avait vu à la question précédente).

On détermine que le coût minimum de production de R est obtenu pour un taux de conversion de A en sortie de 79,48% ; ce coût vaut alors 0,2812 € mol^-1.