Exercice : Optimisation de rendement dans un réacteur siège de trois réactions parallèles [GRC homogène]

Optimisation de rendement dans un réacteur siège de trois réactions parallèles

En milieu aqueux, on met en œuvre le système de réactions suivant :

(1)	A → R	\(r_1 = k_1\)	\(k_1 =\) 1 mol L^-1 h^-1
(2)	A → S	\(r_2 = k_2 \cdot C_A\)	\(k_2 =\) 10 h^-1
(3)	A → T	\(r_3 = k_3 \cdot C_A^2\)	\(k_3 =\) 10 L mol^-1 h^-1

La solution à l'entrée du réacteur ne contient que de l'eau et du réactif A à la concentration \(C_{A0} =\) 1 mol/L. On se propose de mettre en œuvre ces réactions de manière isotherme à 50°C. On désigne par \(X_A\) le taux de conversion de A.

Question

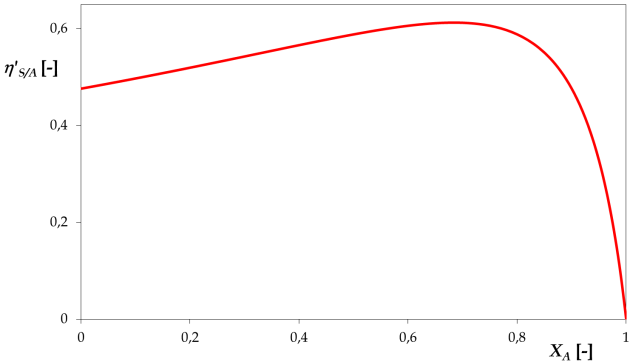
Établir l'expression de la vitesse \(\mathbb{R}_A\) de consommation de A en fonction de \(X_A\) ; ainsi que l'expression du rendement différentiel \(\eta'_{S/A}\). Représenter \(\eta'_{S/A}\) vs \(X_A\) graphiquement.

Résultat

\(\eta'_{S/A} = \frac{k_2 \cdot C_{A0} \cdot \left( 1 - X_A \right)}{k_1 + k_2 \cdot C_{A0} \cdot \left( 1 - X_A \right) + k_3 \cdot C_{A0}^2 \cdot \left( 1 - X_A \right)^2}\)

Solution

En phase liquide, de volume constant, on peut écrire : \(C_A = C_{A0} \cdot \left( 1 - X_A \right)\)

La vitesse de consommation de A est \(- \mathbb{R}_A = r_1 + r_2 + r_3 = k_1 + k_2 \cdot C_{A0} \cdot \left( 1 - X_A \right) + k_3 \cdot C_{A0}^2 \cdot \left( 1 - X_A \right)^2\)

La vitesse de production de S est \(\mathbb{R}_S = r_2 = k_2 \cdot C_{A0} \cdot \left( 1 - X_A \right)\)

On peut obtenir au maximum 1 mole de S à partir d'1 mole de A, donc \(\eta'_{S/A} = \frac{r_2}{r_1 + r_2 + r_3}\)

Soit \(\eta'_{S/A} = \frac{k_2 \cdot C_{A0} \cdot \left( 1 - X_A \right)}{k_1 + k_2 \cdot C_{A0} \cdot \left( 1 - X_A \right) + k_3 \cdot C_{A0}^2 \cdot \left( 1 - X_A \right)^2} = \frac{1 - X_A}{2,1 - 3 \cdot X_A + X_A^2}\)

Question

On désire convertir A à 95% et on utilise à cet effet un réacteur agité continu. Calculer le temps de passage nécessaire ainsi que le rendement opératoire \(Y_{S/A}\) en sortie de réacteur.

Résultat

31% de rendement global ; 37 min de temps de passage

Solution

\(Y_{S/A} = \int\limits_{0}^{X_A^s}{\eta'_{S/A} \left( X_A \right) \cdot \mathrm{d}X_A}\), or dans un RPA, \(X_A\) est le même partout, égal à \(X_A^s\), soit \(Y_{S/A} = \eta'_{S/A} \left( X_A^s \right) \cdot X_A^s = \frac{\left( 1 - X_A^s \right) \cdot X_A^s}{2,1 - 3 \cdot X_A^s + {X_A^s}^2} =\) 0,31, soit 31% de rendement global

Le bilan en A sur le RPA s'écrit \(F_A^e - \mathbb{R}_A \cdot V_{RPA} = F_A^s\), ou encore \(C_A^e - \mathbb{R}_A \cdot \tau_{RPA} = C_A^s\)

D'où \(\tau_{RPA} = \frac{C_{A0} \cdot X_A^s}{k_1 + k_2 \cdot C_{A0} \cdot \left( 1 - X_A^s \right) + k_3 \cdot C_{A0}^2 \cdot \left( 1 - X_A^s \right)} = \frac{X_A^s}{21 - 30 \cdot X_A^s +10 \cdot {X_A^s}^2} =\) 0,62 h, soit 37 min de temps de passage

Question

Mêmes questions pour un réacteur piston.

Résultat

52% de rendement global ; 9,5 min de temps de passage

Solution

\(Y_{S/A} = \int\limits_{0}^{X_A^s}{\eta'_{S/A} \left( X_A \right) \cdot \mathrm{d}X_A}\), l'intégration numérique fournit un rendement opératoire de 0,52, soit 52% de rendement global

Le bilan en A sur le réacteur piston s'écrit \(\mathrm{d}F_A = -\mathbb{R}_A \cdot \mathrm{d}V\), ou encore \(\mathrm{d}C_A = -\mathbb{R}_A \cdot \mathrm{d}\tau\)

D'où \(\tau_{piston} = C_{A0} \cdot \int\limits_{0}^{X_A^s}{\frac{\mathrm{d}X_A}{\mathbb{R}_A}} = C_{A0} \cdot \int\limits_{0}^{X_A^s}{\frac{\mathrm{d}X_A}{k_1 + k_2 \cdot C_{A0} \cdot \left( 1 - X_A \right) + k_3 \cdot C_{A0}^2 \cdot \left( 1 - X_A \right)^2}}\)

L'intégration numérique fournit 0,16 h, soit 9,5 min de temps de passage

Question

Montrer qu'il existe une combinaison optimale de réacteurs idéaux permettant de maximiser le rendement. Calculer le rendement global et le temps de passage pour la combinaison choisie (toujours pour = 0,95).

Résultat

RPA jusqu'à 68,4% de conversion, puis réacteur piston

57% de rendement global ; 13,5 min de temps de passage

Solution

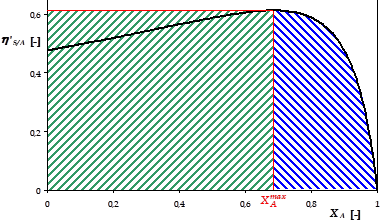
Comme illustré sur la figure précédente, on maximise le rendement opératoire en associant en série un RPA (hachures vertes) pour atteindre le taux de conversion \(X_A^{max}\) puis un réacteur piston (hachures bleues) de \(X_A^{max}\) à \(X_A^s\).

On trouve la valeur de \(X_A^{max}\) en dérivant \(\frac{\mathrm{d}\eta'_{S/A}}{\mathrm{d}X_A} = \frac{-2,1 + 3 \cdot X_A - X_A^2 - \left( 1 - X_A \right) \cdot \left( -3 + 2 \cdot X_A \right)}{\left( 2,1 - 3 \cdot X_A + X_A^2 \right)^2} = \frac{-2,1 + 3 \cdot X_A - X_A^2 + 3 - 2 \cdot X_A - 3 \cdot X_A + 2 \cdot X_A^2}{\left( 2,1 - 3 \cdot X_A + X_A^2 \right)^2} = \frac{0,9 - 2 \cdot X_A + X_A^2}{\left( 2,1 - 3 \cdot X_A + X_A^2 \right)^2}\)

\(X_A^{max}\) est tel que \(0,9 - 2 \cdot X_A^{max} + {X_A^{max}}^2 = 0\), soit \(X_A^{max} =\) 0,684, soit 68,4%

Alors \(Y_{S/A}^{max} = \eta'_{S/A} \left( X_A^{max} \right) \cdot X_A^{max} + \int\limits_{X_A^{max}}^{X_A^s}{\eta'_{S/A} \left( X_A \right) \cdot \mathrm{d}X_A} = \frac{\left( 1 - X_A^{max} \right) \cdot X_A^{max}}{2,1 - 3 \cdot X_A^{max} + {X_A^{max}}^2} + \int\limits_{X_A^{max}}^{X_A^s}{\eta'_{S/A} \left( X_A \right) \cdot \mathrm{d}X_A} =\) 0,42 + 0,15, soit 57% de rendement global

Le temps de passage dans l'ensemble de ces deux réacteurs en série est : \(\tau = \frac{X_A^{max}}{21 - 30 \cdot X_A^{max} + 10 \cdot {X_A^{max}}^2} + \int\limits_{X_A^{max}}^{X_A^s}{\frac{C_{A0} \cdot \mathrm{d}X_A}{k_1 + k_2 \cdot C_{A0} \cdot \left( 1 - X_A \right) + k_3 \cdot C_{A0}^2 \cdot \left( 1 - X_A \right)^2}} =\) 0,133 + 0,093 = 0,225 h, soit 13,5 min de temps de passage

Il resterait à calculer si d'un point de vue économique, il est pertinent de travailler avec deux réacteurs pour gagner 5% de rendement global...