Réacteurs à transformation discontinue des particules
Il s'agit des réacteurs à charge solide non circulante.
Concentration du fluide baignant les particules uniforme et constante
On revient au problème de l'évolution d'un grain unique traité précédemment.
Les particules de taille \(R_0\) ont un taux de conversion \(X_B(R_0,t)\) à chaque instant \(t\).
À chaque instant \(t\), le taux de conversion moyen est tel que : \(\displaystyle 1 - \overline{X_B}(t) = \sum_{R_{0 \; min}}^{R_{0 \; max}} \left[ 1 - X_B(R_0,t) \right] \cdot W(R_0)\).
Si toutes les particules ont la même taille, elles réagissent toutes de manière semblable.
Lit de solide traversé par un fluide en écoulement piston
Attention :
On se limitera au cas d'un solide mono-disperse (une seule taille \(R_0\)).
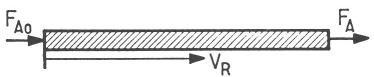
On considère un lit fixe de solide (contenant le réactif solide \(B\)) traversé par un fluide en écoulement piston (contenant le réactif fluide \(A\)).
La position à l'intérieur du lit fixe sera repérée par le volume total \(V_R\) depuis l'entrée du réacteur (volume du fût vide). La fraction de volume occupée par le solide est \((1-\varepsilon)\), où \(\varepsilon\)[1] est la porosité interparticulaire.
Le flux molaire de \(A\) entrant dans le réacteur sera noté \(F_{A0}\) et le flux molaire[2] de \(A\) à une position quelconque dans le réacteur sera noté \(F_A\).
La vitesse de réaction rapportée au volume sera notée \(r_V\). Cette vitesse est une fonction de \(C\), \(X_B\) et \(R_0\).
Les équations aux dérivées partielles à résoudre représentent :
le bilan sur le réactif solide : \(\frac{\partial X_B}{\partial t} = \frac{\nu \cdot M_B}{\rho_B} \cdot r_V\)
le bilan sur le réactif fluide : \(\frac{\partial F_A}{\partial V_R} + \varepsilon \cdot \frac{\partial C_A}{\partial t} + (1-\varepsilon) \cdot r_V = 0\)
avec les conditions limites : \(\begin{cases} en \; V_R=0, F_A=F_ {A0} \\ \grave{a} \; t=0, X_B=0 \end{cases}\)
« CORRIGÉ »
Exemple : Réaction lente
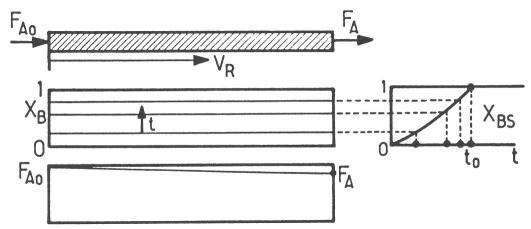
Si la réaction est lente (ou si \(F_{A0}\) est très grand), \(X_B\) et \(F_A \simeq F_{A0}\) sont uniformes et ne dépendent pas de la position \(V_R\), mais seulement de \(t\) ; selon les mêmes expressions que le grain unique traité précédemment.
Exemple : Réaction rapide
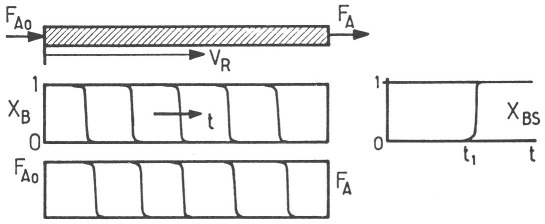
Si la réaction est rapide, \(A\) est consommé totalement à mesure qu'il rencontre du solide \(B\) "frais" : on observe un front de réaction qui avance à vitesse constante dans le lit.
En négligeant le terme d'accumulation \(\frac{\partial C}{\partial t}\), on trouve \(\frac{\partial F_A}{\partial V_R} + \frac{\rho_B \cdot (1-\varepsilon)}{\nu \cdot M_B} \cdot \frac{q}{\Delta V_R} = 0\)
avec \(q\) le débit de déplacement du front de réaction et \(\Delta V_R\) l'épaisseur de la zone réactionnelle. Sur cette épaisseur \(\Delta V_R\), \(F_A\) passe de \(F_{A0}\) à 0 et \(X_B\) passe de 0 à 1. Ceci se fait dans le temps \(\Delta t = \frac{\Delta V_R}{q}\).
On a donc \(\frac{F_{A0}}{\Delta V_R} + \frac{\rho_B \cdot (1-\varepsilon)}{\nu \cdot M_B} \cdot \frac{q}{\Delta V_R} = 0\)
Le débit de déplacement du front de réaction vaut donc \(q = \frac{\nu \cdot M_B \cdot F_{A0}}{\rho_B \cdot (1-\varepsilon)}\).
Le front de réaction ressort du réacteur au bout du temps \(t_1 = \frac{V_R}{q} = \frac{V_R \cdot \rho_B \cdot (1-\varepsilon)}{\nu \cdot M_B\cdot F_{A0}}\).
« CORRIGÉ »
Réaction modérée
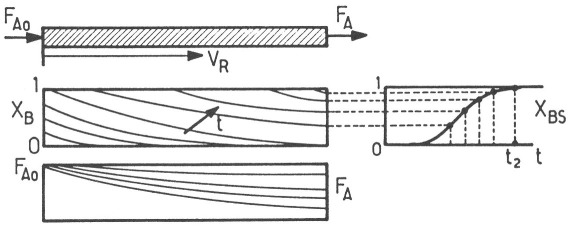
Si la vitesse de réaction n'est ni particulièrement rapide ni très lente, il faut intégrer numériquement le système d'équations aux dérivées partielles écrit précédemment.
Lit de solide traversé par un fluide en mélange parfait
C'est typiquement le cas d'un lit fluidisé avec solide non circulant.
Attention :
On se limitera au cas d'un solide mono-disperse (une seule taille \(R_0\)).
Le taux de conversion du solide \(X_B\) et l'évolution au cours du temps de la concentration en réactif fluide \(C\) sont obtenus par résolution simultanée :
du bilan sur le réactif solide : \(\frac{\mathrm{d} X_B}{\mathrm{d} t} = \frac{\nu \cdot M_B}{\rho_B} \cdot r_V\)
et du bilan sur le réactif fluide : \(F_{A0} - (1-\varepsilon) \cdot r_V \cdot V_R = F_A + \varepsilon \cdot V_R \cdot \frac{\mathrm{d} C}{\mathrm{d} t}\)
« CORRIGÉ »
Exemple :
Dans le cas particulier où \(A\) est très réactif et \(B\) est en excès, \(F_A \rightarrow 0\).
Si on peut négliger le terme en \(\frac{\mathrm{d} C}{\mathrm{d} t}\), on obtient en combinant les deux bilans précédents \(\frac{\mathrm{d} X_B}{\mathrm{d} t} = \frac{\nu \cdot M_B\cdot F_{A0}}{\rho_B \cdot (1-\varepsilon)}\).
Si \(F_{A0}\) est contant, \(X_B\) augmente linéairement en fonction du temps jusqu'au temps \(t_1 = \frac{V_R \cdot \rho_B \cdot (1-\varepsilon)}{\nu \cdot M_B \cdot F_{A0}}\) de conversion totale, qui n'est autre que le temps stœchiométrique au bout duquel on a apporté au solide tout le réactif nécessaire pour le convertir.
« CORRIGÉ »
Ce calcul s'applique par exemple au traitement en lit fluidisé semi-continu (assimilé à un mélangeur parfait) d'une charge solide qui demeure dans le réacteur, par un débit constant de réactif gazeux.