Transfert gaz/liquide avec réaction chimique

Voyons comment on peut définir les principaux nombres adimensionnels caractéristiques du système :

  • critère de Hatta \(Ha\),

  • facteur d'accélération \(E_A\).

vidéo : transfert fluide-fluide avec réaction chimiqueInformations[1]

Raisonnement

\(z\) étant positionné sur un axe perpendiculaire à l'interface gaz/liquide,

  • le flux molaire de \(A\) par unité de volume entrant dans une tranche d'épaisseur \(\mathrm{d} z\) du film liquide est \(- a \cdot D_A \cdot \frac{\mathrm{d} C_A}{\mathrm{d} z}\), où \(a\) est l'aire interfaciale[2] (rapport de la surface de l'interface sur le volume du réacteur) et \(D_A\) le coefficient de diffusion de \(A\) en phase liquide ;

  • le flux molaire de \(A\) par unité de volume sortant de cette tranche est \(- a \cdot D_A \cdot \left( \frac{\mathrm{d} C_A}{\mathrm{d} z} + \frac{\mathrm{d}^2 C_A}{\mathrm{d} z^2} \cdot \mathrm{d} z \right)\) ;

  • le flux molaire de \(A\) par unité de volume consommé par la réaction est \(- k \cdot C_A \cdot {C_B}^n \cdot a \cdot \mathrm{d} z\)., où \(k\) est la constante de vitesse de réaction[3].

Ainsi :

  • le bilan de matière sur l'espèce \(A\) initialement présente en phase gazeuse s'écrit \(D_A \cdot \frac{\mathrm{d}^2 C_A}{\mathrm{d} z^2} = k \cdot C_A \cdot {C_B}^n\) ;

  • le bilan de matière sur l'espèce \(B\) présente uniquement en phase liquide s'écrit \(D_B \cdot \frac{\mathrm{d}^2 C_B}{\mathrm{d} z^2} = \nu \cdot k \cdot C_A \cdot {C_B}^n\), où \(D_B\) est le coefficient de diffusion de \(B\) en phase liquide.

Les conditions limites de ces deux équations différentielles sont :

  • en \(z = 0\), \(C_A = C_{Ai}\) (qui suit la loi de HENRY) et \(\frac{\mathrm{d} C_B}{\mathrm{d} z} = 0\) (car l'espèce \(B\) ne s'évapore pas) ;

  • en \(z = \delta\) (\(\delta\) étant l'épaisseur du film liquide[4]), \(C_B = C_{BL}\) et \(-a \cdot D_A \cdot \frac{\mathrm{d} C_A}{\mathrm{d} z} = k \cdot C_{AL} \cdot {C_{BL}}^n \cdot \left( \epsilon_L - a \cdot \delta \right)\), où \(\epsilon_L\) est la rétention liquide[5] (rapport du volume liquide sur le volume du réacteur). Le membre de gauche de cette dernière condition limite correspond au flux molaire de \(A\) par unité de volume qui sort du film par diffusion et le membre de droite au flux molaire par unité de volume consommé par réaction, pour lequel on retire le volume du film.

Rappel

D'après le modèle de WHITMAN, \(k_L = \frac{D_A}{\delta}\).

Définitionnombre de HATTA

On définit le nombre (ou critère) de HATTA \(Ha\)[6], tel que \(Ha^2 = \frac{\delta^2 \cdot k \cdot {C_{BL}}^n}{D_A} = \frac{k \cdot {C_{BL}}^n \cdot D_A}{{k_L}^2}\).

On définit également les grandeurs réduites : \(x = \frac{z}{\delta}\) ; \(\mathbb{C}_A = \frac{C_A}{C_{Ai}}\) ; \(\mathbb{C}_B = \frac{C_B}{C_{BL}}\).

Raisonnement

Les bilans précédents et leurs conditions limites deviennent alors :

\[\left\{ \begin{array} {l} \frac{\mathrm{d}^2 \mathbb{C}_A}{\mathrm{d} x^2} =Ha^2 \cdot \mathbb{C}_A \cdot {\mathbb{C}_B}^n \\ \frac{\mathrm{d}^2 \mathbb{C}_B}{\mathrm{d} x^2} = \nu \cdot \frac{D_B}{D_A} \cdot \mathbb{C}_A \cdot {\mathbb{C}_B}^n \\ \mathrm{en \:} x = 0, \; \frac{\mathrm{d} \mathbb{C}_B}{\mathrm{d} x} = 0 \; \mathrm{et \;} \mathbb{C}_A = 1\\ \mathrm{en \:} x = 1, \; \mathbb{C}_B = 1 \; \mathrm{et \;} \; - \frac{\mathrm{d} \mathbb{C}_A}{\mathrm{d} x} = f \cdot \ Ha^2 \cdot (\beta - 1) \end{array} \right.\]

où \(\beta = \frac{\epsilon_L}{a \cdot \delta}\) et \(f = \frac{C_{AL}}{C_{Ai}}\).

Notion fondamentale

Ce système d'équations différentielles ne peut être résolu que numériquement dans le cas général. Dans certains cas particuliers, il peut exister une solution analytique.

Exemplediffusion de A dans le film limitante

Lorsque la diffusion de \(A\) dans le film est limitante, \(C_{AL} \approx 0\) (car la réaction est rapide comparativement à la diffusion).

Le flux volumique de transfert de \(A\) est alors \(\Phi_1 \approx k_L \cdot a \cdot C_{Ai}\).

Exempleréaction chimique lente

Lorsque la réaction chimique est lente, \(C_B \approx C_{BL}\) (il y a peu de consommation de \(B\) dans le film).

Le bilan en \(A\) s'écrit : \(D_A \cdot \frac{\mathrm{d}^2 \mathbb{C}_A}{\mathrm{d} x^2} \approx k' \cdot \mathbb{C}_A\), où \(k' = k \cdot {\mathbb{C}_B}^n\) est une constante.

Cette équation différentielle n'est plus couplée au bilan en \(B\) et peut être résolue avec ses conditions limites. La solution est \(\mathbb{C}_A (x)= \mathbb{C}_{Ai} \cdot \exp \left( - \sqrt{ \frac{k'}{D_A} } \cdot x \right)\) et le flux volumique de transfert de \(A\) est alors \(\Phi_2 \approx \sqrt{k' \cdot D_A} \cdot a \cdot C_{Ai}\).

Notion fondamentale

On retrouve que \(\frac{\Phi_2}{\Phi_1} = \frac{ \mathrm{flux \: maximal \: de \: r \acute{e} action} }{ \mathrm{flux \: maximal \: transf \acute{e} rable \: dans \: le \: film} } = \frac{\sqrt{k \cdot {C_B}^n \cdot D_A}}{k_L}= Ha\).

Lorsque le nombre de HATTA est faible (classiquement \(Ha < 0,3\)), la réaction au sein du liquide est très lente. Afin de favoriser la réaction, il faut un grand volume liquide ; il n'est pas utile de promouvoir le transfert gaz/liquide et donc de générer une grande aire interfaciale. C'est le régime chimique[7].

Au contraire, lorsque le nombre de HATTA est grand (classiquement \(Ha > 3\)), la réaction au sein du liquide est rapide et a lieu essentiellement dans le film liquide. Pour favoriser la réaction, il faut générer une grande aire interfaciale afin de promouvoir le transfert gaz/liquide ; il n'est pas utile d'avoir un grand volume liquide. C'est le régime diffusionnel[8].

Dans le cas général, le flux volumique de transfert de \(A\) est donné par \(\Phi = k_L \cdot a \cdot C_{Ai} \cdot E_A\), où \(E_A\) est le facteur d'accélération, qui représente le rapport entre le flux de \(A\) et le flux de \(A\) en l'absence de réaction.

Avec les résistances en série, on obtient \(\Phi = \frac{P_A}{ \frac{1}{k_g \cdot a} + \frac{He}{k_L \cdot a \cdot E_A} + \frac{He}{k \cdot \epsilon_L \cdot {C_{BL}}^n} }\).

La première fraction au dénominateur correspond à la résistance au transfert dans le film côté gaz ; la deuxième correspond à la résistance au transfert + réaction dans le film côté liquide ; la troisième correspond à la résistance liée à la réaction dans le liquide.

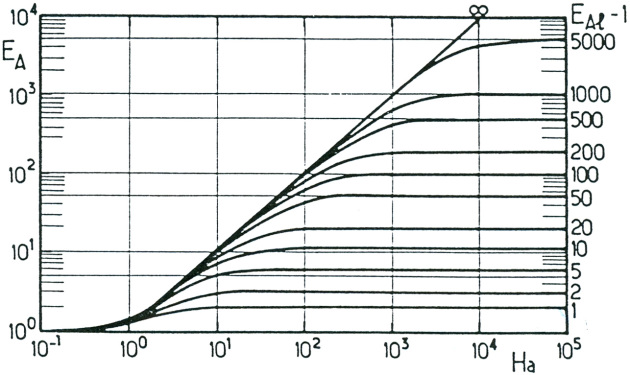
Le facteur d'accélération peut être obtenu par la relation implicite de VAN KREVELEN ci-dessous.

\[E_A = \frac{Ha \cdot {\left( \frac{E_{Al}-E_A}{E_{Al}-1} \right)}^{1/2}}{\mathrm{th \:} \left[ Ha \cdot { \left( \frac{E_{Al}-E_A}{E_{Al}-1} \right) }^{1/2} \right] }\]

où le facteur d'accélération limite vaut \(E_{Al} = 1 + \frac{D_B \cdot C_{BL}}{\nu \cdot D_A \cdot C_{Ai}}\).

Le facteur d'accélération peut également être lu sur l'axe vertical de gauche du diagramme ci-dessous, où on portera en abscisse la valeur du nombre de HATTA et sur lequel on trouve diverses courbes correspondant à la valeur de \(E_{Al} - 1\) portée sur l'axe vertical de droite.

Diagramme de VAN KREVELEN.Informations[9]

Définitionrapport R et nombre de DAMKÖHLER

On définit également :

  • le rapport \(R\)[10] = \(\frac{ \mathrm{flux \: maxi \: de \:} A \: \mathrm{consommable \: par \: r \acute{e} action} }{ \mathrm{flux \: maxi \: de \:} A \: \mathrm{absorable \: physiquement} } = \frac{k \cdot {C_{BL}}^n \cdot \epsilon_L}{k_L \cdot a}\) ; si \(R\) est petit, la réaction est lente par rapport à ce qui peut être absorbé ; inversement, si \(R\) est supérieur à 10, la concentration en gaz dissous dans le liquide peut être considéré comme nulle ;

  • le nombre de DAMKÖHLER[11], qui est le rapport entre le temps caractéristique du transfert de matière (\(\frac{1}{k_L \cdot a}\)) et le temps de contact entre les phases dans le réacteur (qui n'est autre que le temps de passage \(\frac{V_{r \acute{e} acteur}}{Q_v}\)) ; ainsi \(Da = k_L \cdot a \cdot \frac{V_{r \acute{e} acteur}}{Q_v}\), où \(Q_v\) est le débit volumique total (gaz + liquide). Si \(Da\) est petit (typiquement \(<< 1\)), le temps de passage est trop court par rapport au phénomène de transfert de matière.

Pour aller plus loinfacteurs influençant le transfert de matière