Modèle à cœur rétrécissant
Ce modèle de réaction met en jeu les étapes suivantes du processus réactionnel :
approche du fluide réactif de la surface extérieure du grain solide ;
diffusion du fluide réactif à l'intérieur de la couche poreuse de cendres ;
réaction chimique du réactif fluide avec le solide (il s'agit souvent d'une réaction de surface impliquant un mécanisme d'adsorption/désorption ;
diffusion du produit fluide (lorsqu'il existe) à travers les cendres poreuses vers la surface externe du grain ;
dispersion du produit fluide (lorsqu'il existe) dans la phase fluide.
Les deux dernières étapes n'ont d'importance que dans le cas où la réaction est équilibrée. Nous n'envisagerons ici que des réactions irréversibles.
Attention :
On suppose que :
la réaction a lieu à l'interface cendre/cœur (trait vert sur la figure ci-dessous) ;
la température est uniforme ;
la taille des particules reste inchangée (rayon \(R_0\) constant) ;
la composition \(C_B = \frac{\rho_B}{M_B}\)[2] du solide réactif reste constante (cœur vert pâle sur la figure ci-dessous).
Les principales notations utilisées sont résumées sur le schéma ci-dessous.

\(R_0\) est le rayon (supposé constant) de la particule.
\(R_c\)[4] est le rayon du cœur solide \(B\) qui n'a pas encore réagit (c'est donc la position du front de réaction) : il diminue au cours du temps.
\(R\) est le rayon définissant une position quelconque dans les cendres poreuses adhérentes (il est compris entre \(R_c\) et \(R_0\)).
\(C_e\) est la concentration en réactif \(A\) dans la phase fluide loin de la particule.
\(C_s\) est la concentration en réactif \(A\) à la surface externe de la particule (au niveau du trait continu rouge sur la figure ci-dessus).
\(C_c\) est la concentration en réactif \(A\) à l'interface entre le cœur solide \(B\) non converti et les cendres (au niveau du trait vert sur la figure ci-dessus).
Définition : Taux de conversion
On définit le taux de conversion par rapport au solide réactif B[5] : \(n_B = n_{B0} \cdot (1-X_B)\).
On peut également l'écrire : \(1-X_B = \frac{\frac{4}{3} \pi {R_c}^ 3 \cdot \frac{\rho_B}{M_B}}{\frac{4}{3} \pi R_0^ 3 \cdot \frac{\rho_B}{M_B}} = { \left( \frac{R_c}{R_0} \right)}^3\) puisque la composition \(\frac{\rho_B}{M_B}\) du solide réactif est supposée constante.
Par conséquent \(\frac{R_c}{R_0} = (1-X_B)^{1/3}\).
Dans la couche de cendres, l'équation de bilan matière relative au composé \(A\) s'écrit :
\(\epsilon_p \cdot \frac{\partial C}{\partial t} = D_e \cdot \left( \frac{\partial^2 C}{\partial R^2} + \frac{2}{R} \cdot \frac{\partial C}{\partial R} \right)\) pour \(R_c < R < R_0\)
Avec les conditions limites suivantes :
à la surface de la particule, en \(R=R_0\) : \(D_e \cdot {\left( \frac{\partial C}{\partial R} \right)}_{R=R_0} = k_D \cdot (C_e - C_s)\)
à la surface du cœur (interface entre les cendres et le réactif solide \(B\) qui n'a pas encore réagi), en \(R=R_c\) : \(D_e \cdot {\left( \frac{\partial C}{\partial R} \right)}_{R=R_c} = k" \cdot C_c^n\)
Régime contrôlé par le transport externe
Raisonnement :
Si le régime est contrôlé par le transport externe[6], \(C_s\) et \(C_c\) sont à peu près égales et tendent vers zéro (la limitation étant au niveau du transport externe, dès que \(A\) a pu parvenir à la surface du grain, il traverse sans difficulté la couche de cendre et réagit en surface du cœur).
Le flux[7] de \(A\) transféré s'obtient en multipliant la densité de flux du transport externe par la surface externe du grain : \(F_A = 4 \pi R_0^2 \cdot k_D \cdot (C_e - C_s) \simeq 4 \pi R_0^2 \cdot k_D \cdot C_e\) puisque \(C_s \simeq 0\).
Compte tenu de la stœchiométrie de la réaction, on a également \(F_A = \frac{-1}{\nu} \cdot \frac{\mathrm{d} n_B}{\mathrm{d} t} = \frac{-1}{\nu} \cdot \frac{\rho_B}{M_B} \cdot \frac{\mathrm{d} V_B}{\mathrm{d} t}\) puisque la composition \(\frac{\rho_B}{M_B}\) du solide réactif reste constante.
Finalement \(F_A = \frac{-1}{\nu} \cdot \frac{\rho_B}{M_B} \cdot 4 \pi {R_c}^2 \cdot \frac{\mathrm{d} R_c}{\mathrm{d} t} \simeq 4 \pi R_0^2 \cdot k_D \cdot C_e\), que l'on peut intégrer -avec \(F_A\) constant en régime permanent- selon : \(\displaystyle \nu \cdot \frac{R_0^2 \cdot M_B \cdot k_D \cdot C_e}{\rho_B} \cdot \int_0^t \mathrm{d} t = - \int_{R_0}^{R_c} R^2 \cdot \mathrm{d} R\), soit \(\nu \cdot \frac{R_0^2 \cdot M_B \cdot k_D \cdot C_e}{\rho_B} \cdot t = \frac{1}{3} \cdot \left( R_0^3 - {R_c}^3 \right)\), soit \(t = \frac{\rho_B \cdot R_0}{3 \cdot \nu \cdot M_B\cdot k_D \cdot C_e} \cdot \left[ 1 - { \left( \frac{R_c}{R_0} \right)}^3 \right] = \frac{\rho_B \cdot R_0}{3 \cdot \nu \cdot M_B \cdot k_D \cdot C_e} \cdot X_B\), puisque \(X_B = 1 - {\left( \frac{R_c}{R_0} \right)}^3\).
Notion fondamentale : Temps de conversion en régime contrôlé par le transport externe
En régime contrôlé par le transport externe,
\(\tau_{ext}\)[8] = \(\frac{\rho_B \cdot R}{3 \cdot \nu \cdot M_B \cdot k_D \cdot C_e}\) est le temps de conversion complète (également appelé temps caractéristique du transfert externe)
et \(t = \tau_{ext} \cdot X_B\) est le temps nécessaire pour obtenir une conversion \(X_B\) donnée.
Régime contrôlé par la diffusion dans les cendres
Raisonnement :
Si le régime est contrôlé par la diffusion dans les cendres[9], \(C_s \simeq C_e\) puisque le transport externe est facile et \(C_c \rightarrow 0\) puisque la réaction est rapide.
Le flux de \(A\) transféré s'obtient en multipliant la densité de flux du transfert interne -à une position \(r\) quelconque dans les cendres- par la surface à cette position \(r\) : \(F_A = 4 \pi R^2 \cdot D_e \cdot \frac{\mathrm{d} C}{\mathrm{d} R}\). \(F_A\) étant constant en régime permanent, on peut intégrer : \(\displaystyle \frac{F_A}{D_e} \cdot \int_{R_0}^{R_c} \frac{\mathrm{d} R}{4 \pi R^2} = \int_{C_e}^0 \mathrm{d} C\), soit \(\frac{F_A}{4 \pi D_e} \cdot \left( \frac{1}{R_0} - \frac{1}{R_c} \right) = - C_e\) et donc \(F_A = 4 \pi D_e \cdot C_e \cdot \frac{R_c \cdot R_0}{R_0-R_c}\).
Par ailleurs, toujours compte tenu de la stœchiométrie de la réaction, on a \(F_A = \frac{-1}{\nu} \cdot \frac{\mathrm{d} n_B}{\mathrm{d} t} = \frac{-4 \pi \cdot {R}^2}{\nu} \cdot \frac{\rho_B}{M_B} \cdot \frac{\mathrm{d} R}{\mathrm{d} t}\) où on peut remplacer \(F_A\) puis intégrer en \(\displaystyle - \int_{R_0}^{R_c} {\frac{R_c}{R_0} \cdot (R_0-R) \cdot \mathrm{d} R} = \frac{\nu \cdot M_B \cdot D_e \cdot C_e}{\rho_B} \cdot \int_0^t \mathrm{d} t\).
Or \(\displaystyle - \int_{R_0}^{R_c} {\frac{R_c}{R_0} \cdot (R_0-R) \cdot \mathrm{d} R} = \int_{R_0}^{R_c} R \cdot \mathrm{d} R - \frac{1}{R_0} \cdot \int_{R_0}^{R_c} R^2 \cdot \mathrm{d} R = \frac{R_0^2-{R_c}^2}{2} - \frac{1}{R_0} \cdot \frac{R_0^3-{R_c}^3}{3}\), soit \(t = \frac{\rho_B \cdot R_0^2}{\nu \cdot M_B \cdot D_e \cdot C_e} \cdot \left( \frac{1}{2} \cdot \left[ 1 - {\left( \frac{R_c}{R_0} \right)}^2 \right] - \frac{1}{3} \cdot \left[ 1 - {\left( \frac{R_c}{R_0} \right)}^3 \right] \right)\).
Et comme \(\frac{R_c}{R_0} = {\left( 1 - X_B \right)}^{1/3}\), on a \(\frac{1}{2} \cdot \left[ 1 - {\left( \frac{R_c}{R_0} \right)}^2 \right] - \frac{1}{3} \cdot \left[ 1 - {\left( \frac{R_c}{R_0} \right)}^3 \right] = \frac{1}{6} \cdot \left[ 1 - 3 \cdot (1-X_B)^{2/3} + 2 \cdot(1-X_B) \right]\).
Finalement \(t = \frac{\rho_B \cdot R_0^2}{6 \cdot \nu \cdot M_B\cdot D_e \cdot C_e} \cdot \left[ 1 - 3 \cdot (1-X_B)^{2/3} + 2 \cdot(1-X_B) \right]\).
Notion fondamentale : Temps de conversion en régime contrôlé par la diffusion dans les cendres
En régime contrôlé par la diffusion dans les cendres,
\(\tau_{diff}\)[10] = \(\frac{\rho_B \cdot R_0^2}{6 \cdot \nu \cdot M_B \cdot D_e \cdot C_e}\) est le temps de conversion complète (également appelé temps caractéristique de la diffusion interne)
et \(t = \tau_{diff} \cdot \left[ 1 - 3 \cdot (1-X_B)^{2/3} + 2 \cdot(1-X_B) \right]\) est le temps nécessaire pour obtenir une conversion \(X_B\) donnée .
Régime chimique
Raisonnement :
Si le régime est contrôlé par la réaction[11], \(C_e \simeq C_s \simeq C_c\) puisqu’à la fois le transport externe et la diffusion interne sont très faciles.
Le flux de \(A\) transféré s'obtient en multipliant la densité de flux correspondant à la réaction par la surface du cœur : \(F_A = 4 \pi {R_c}^2 \cdot k" \cdot C_e^n = \frac{-4 \pi \cdot {R_c}^2}{\nu} \cdot \frac{\rho_B}{M_B} \cdot \frac{\mathrm{d} R}{\mathrm{d} t}\), soit \(k" \cdot C_e^n = - \frac{\rho_B}{\nu \cdot M_B} \cdot \frac{\mathrm{d} R}{\mathrm{d} t}\), que l'on intègre : \(\displaystyle t = \int_0^t \mathrm{d} t = - \frac{\rho_B}{\nu \cdot M_B \cdot k" \cdot C_e^n} \cdot \int_{R_0}^{R_c} \mathrm{d} R = \frac{\rho_B \cdot R_0}{\nu \cdot M_B \cdot k" \cdot C_e^n} \cdot \left( 1 - \frac{R_c}{R_0} \right)\).
Notion fondamentale : Temps de conversion en régime chimique
En régime chimique,
\(\tau_{chim}\)[12] = \(\frac{\rho_B \cdot R_0}{\nu \cdot M_B\cdot k" \cdot C_e^n}\) est le temps de conversion complète (également appelé temps caractéristique de la réaction chimique)
et \(t = \tau_{chim} \cdot \left[ 1 - (1-X_B)^{1/3} \right]\) est le temps nécessaire pour obtenir une conversion \(X_B\) donnée.
Cas général
Lorsqu'aucune limitation n'est prépondérante, il faut tenir compte de toutes les étapes du processus réactionnel.
Raisonnement :
En régime permanent, le flux de \(A\) transféré est identique pour toutes les étapes : \(F_A =\begin{cases} 4 \pi {R_c}^2 \cdot k" \cdot C_c^n \\ 4 \pi \cdot D_e \cdot \frac{C_s - C_c}{ \frac{1}{R_c} - \frac{1}{R_0}} \\ 4 \pi R_0^2 \cdot k_D \cdot (C_e - C_s) \end{cases}\)
En divisant tout par \(4 \pi R_0^2\), on obtient la densité de flux à la surface du grain (position \(R_0\)) : \(N_A|_{R_0}=\frac{C_e - C_s}{\frac{1}{k_D}}=\frac{C_s - C_c}{\frac{R_0 \cdot (R_0-R_c)}{D_e \cdot R_c}}= \frac{C_c^n}{\frac{R_0^2}{k" \cdot {R_c}^2}}\).
Si la réaction est d'ordre \(n=1\), alors \(N_A|_{R_0} =\frac{C_e}{\frac{1}{k_D} + \frac{R_0 \cdot (R_0-R_c)}{D_e \cdot R_c} + \frac{R_0^2}{k" \cdot {R_c}^2}}\) (association de résistances en série).
On a toujours \(F_A = 4 \pi R_0^2 \cdot N_A|_{R_0}= - \frac{1}{\nu} \cdot 4 \pi {R_c}^2 \cdot \frac{\rho_B}{M_B} \cdot \frac{\mathrm{d} R}{\mathrm{d} t}\), dont l'intégration fournit : \(t = \frac{\rho_B \cdot R_0}{\nu \cdot M_B\cdot C_e} \cdot \left[ \frac{1}{3} \cdot \left( \frac{1}{k_D} - \frac{R_0}{D_e} \right) \cdot \left[ 1 - {\left(\frac{R_0}{R_c}\right)}^3 \right] + \frac{R_0}{2 \cdot D_e} \cdot \left[ 1 - {\left(\frac{R_0}{R_c}\right)}^2 \right] + \frac{1}{k"} \cdot \left[ 1 - \left(\frac{R_0}{R_c}\right) \right] \right]\)
Notion fondamentale : Loi des temps caractéristiques additifs
Le temps de conversion complète dans le cas général est \(\tau\)[13] = \(\frac{\rho_B \cdot R_0}{\nu \cdot M_B \cdot C_e} \cdot \left[ \frac{1}{3 \cdot k_D} + \frac{R_0}{6 \cdot D_e} + \frac{1}{k"} \right]\).
On remarque que \(\tau = \tau_{ext} + \tau_{diff} + \tau_{chim}\). C'est la loi des temps caractéristiques additifs : rigoureusement vraie pour les cinétiques d'ordre 1 et approximativement juste lorsque \(n \neq 1\).
Méthode : Temps de conversion dans le cas général
Le temps nécessaire pour obtenir une conversion \(X_B\) donnée est donc :
\(t = \tau \cdot \left[ \left[ 1 - {(1-X_B)}^{1/3} \right] + \frac{k"}{3 \cdot k_D} \cdot X_B + \frac{k" \cdot R_0}{6 \cdot D_e} \cdot \left[ 1 - 3 \cdot (1-X_B)^{2/3} + 2 \cdot (1-X_B) \right] \right]\)
Remarque :
On retrouve évidemment les cas particuliers vus précédemment :
lorsque le transport externe est limitant : \(3 \cdot k_D \ll k"\) et \(k_D \ll 2 \cdot \frac{D_e}{R_0}\) ;
lorsque la diffusion dans le cendres contrôle le processus : \(2 \cdot \frac{D_e}{R_0} \ll k_D\) et \(6 \cdot \frac{D_e}{R_0} \ll k"\);
lorsque la réaction chimique est le phénomène limitant : \(k" \ll 6 \cdot \frac{D_e}{R_0}\) et \(k" \ll 3 \cdot k_D\).
Simulation :
La vitesse de réaction observée est toujours inférieure aux vitesses obtenues avec une seule étape limitante.
Attention :
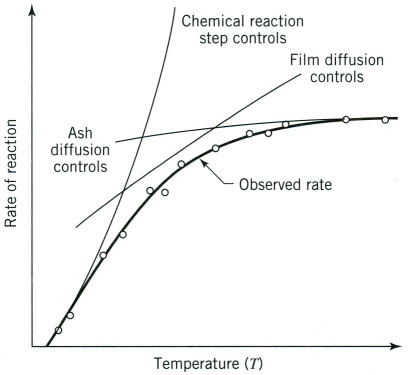
Si la température change (et dans une moindre mesure la taille des grains), l'étape limitante peut évoluer.
Identification expérimentale de l'étape limitante
Expérience :
On peut réaliser des expériences à différentes températures : la réaction chimique est plus sensible à la température que les étapes physiques.
Expérience :
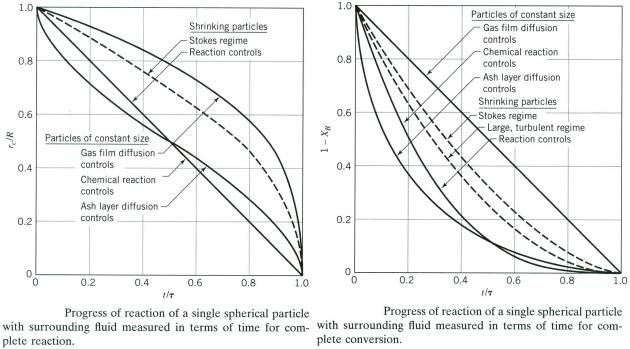
On peut comparer des courbes \(\frac{R_c}{R_0}\) vs \(t\) ou bien \((1-X_B)\) vs \(t\) :
Mais ces courbes étant très proches et leur discrimination est difficile compte tenu de l'erreur expérimentale.