Analyse Dimensionnelle sur un vortex

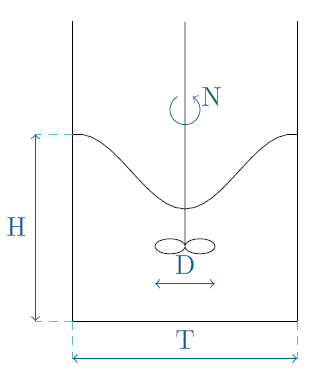
On désire déterminer la hauteur de remontée \(H\) du liquide le long de la paroi au cours de la formation d'un vortex dans une cuve de dissolution de pigments de peinture. Pour ce faire on désire utiliser une maquette de petite taille. Les variables du problème sont les grandeurs géométriques \(H\), \(D\) et \(T\), auxquelles s'ajoutent \(N\)[1], la vitesse de rotation de l'agitateur, les propriétés du fluide \(\rho\) (masse volumique) et \(\mu\) (viscosité dynamique), ainsi que l'accélération de la pesanteur \(g\) qui intervient dans ce genre de problème.

Informations[2]

Question

On utilisera la méthode de Buckingham pour faire apparaître le nombre de Reynolds d'agitation et le nombre de Froude.

\[Re_A=\frac{\rho N D^2}{\mu}\]
\[Fr=\frac{N^2D}{g}\]

Indice

Bien lister les grandeurs et donner leur dimension.

Indice

S'inspirer des nombres adimensionnels présentés pour choisir le représentant de chaque dimension.

Solution

On référence les paramètres :

\[[D]=L \\ [T]=L \\ [H]=L \\ [N]=T^{-1} \\ [\rho]=M.L^{-3} \\ [\mu]=M.L^{-1}.T^{-1} \\ [g]=L.T^{-2}\]

On choisit comme représentant \(D\), \(N\) et \(\rho\).

\[\Pi_1=\frac{T}{D^\alpha N^\beta \rho^\gamma}\]

On trouve assez facilement un nombre adimensionnel en divisant une longueur par une autre longueur donc : \(\Pi_1=\frac{T}{D}\)

\(\Pi_2=\frac{H}{D^\alpha N^\beta \rho^\gamma}\) de la même manière : \(\Pi_1=\frac{H}{D}\)

\(\Pi_3=\frac{\mu}{D^\alpha N^\beta \rho^\gamma}\) et donc :

\(\left\{ \begin{array} {c @{=} c}1 & \gamma \\-1 & \alpha-3\gamma \\-1 & -\beta\end{array} \right.\)

On obtient facilement :  \(\Pi_3=\frac{\mu}{D^2 N \rho}\)

\(\Pi_4=\frac{g}{D^\alpha N^\beta \rho^\gamma}\) et donc :

\(\left\{ \begin{array} {c @{=} c}0 & \gamma \\1 & \alpha-3\gamma \\-2 & -\beta\end{array} \right.\)

on obtient facilement : \(\Pi_3=\frac{g}{D N^2}\)

Donc on trouve bien : \(Re_A=\frac{1}{\Pi_3}\) et \(Fr=\frac{1}{\Pi_4}\)