Exploitation quantitative de la DTS : modélisation
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Ayant obtenu par la méthode des traceurs une courbe expérimentale de DTS[2], on se propose de rendre compte de l'allure observée au moyen d'un modèle hydrodynamique simple, utilisable commodément par la suite pour prédire la conversion chimique d'un réacteur ou pour servir de base à son extrapolation.
Modèle de cascade de RPA
Lorsque \(J\) réacteurs parfaitement agités sont associés en cascade (c'est-à-dire en série), la DTS[2] est la suivante :
\(E\ \left( t_s \right) = {\left( \frac{J}{\overline{t_s}} \right)}^J \cdot \frac{{t_s}^{J-1} \cdot \exp \ \left( -J \frac{t_s}{\overline{t_s}} \right)}{\left( J-1 \right)\ !}\)
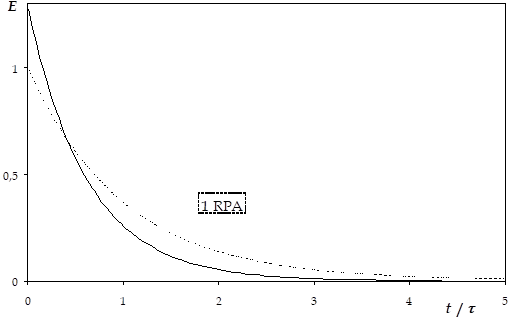
Ce modèle est illustré sur la figure suivante.
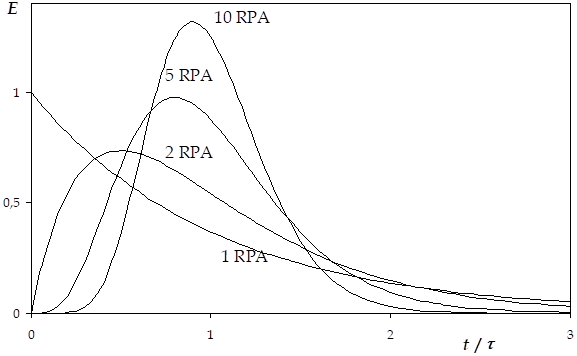
On retrouve le cas du mélangeur parfait pour \(J = 1\) et le piston parfait pour \(J\) infini (dans la pratique pour \(J > 100\)).
Complément : Lien entre les deux modèles
Ces deux modèles sont de natures différentes, en particulier la matière peut remonter le courant (diffusion) dans le cas "dispersion axiale" mais pas dans le cas "cascade de RPA". Toutefois, à \(\text{Pe}\) et \(J\) élevés, ces modèles coïncident, comme on le remarque sur la figure suivante. On a alors \(\text{Pe} = 2 \cdot (J-1)\).
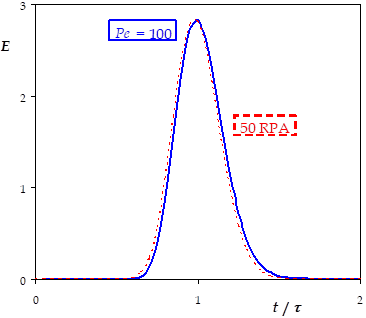
Ces deux modèles permettent une interpolation continue entre les deux cas idéaux que sont le piston et le mélangeur parfaits.
Représentation d'un réacteur réel
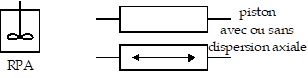
Pour rendre compte du comportement de réacteurs réels où l'écoulement est complexe, on est amené à compliquer les modèles élémentaires (figurés ci-dessus) en les associant (selon les possibilités de la figure suivante).
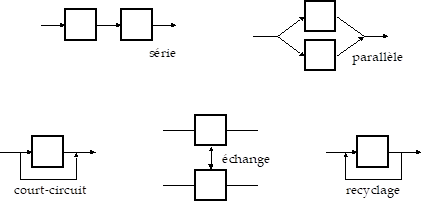
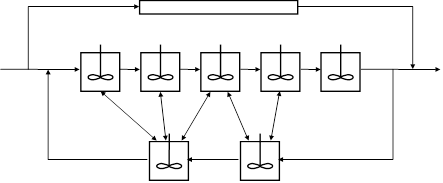
On dit qu'une association de réacteurs idéaux (par exemple celle de la figure suivante) est représentative d'un réacteur réel, et on l'appelle modèle, si les courbes de répartition des temps de séjour des molécules qui les traversent sont identiques. La courbe relative à l'association est calculée et la courbe relative au réacteur est obtenue expérimentalement en utilisant la technique des traceurs. Ce modèle n'est pas toujours unique, notamment pour les écoulements complexes.
Remarque : Représentation des défauts d'écoulement
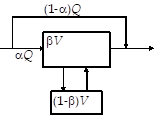
La figure ci-contre présente le modèle de Cholette et Cloutier. Le paramètre \(\alpha\) permet de rendre compte des courts-circuits et le paramètre \(\beta\) des zones stagnantes (recirculations).
La fonction DTS associée est :
\(E\ (t) = ( 1 - \alpha ) \cdot \delta (t) + \frac{\alpha^2}{\beta \cdot \overline{t_s}} \cdot \exp \ \left( -\frac{\alpha \cdot t}{\beta \cdot \overline{t_s}} \right)\)
La figure suivante représente la DTS[2] pour des valeurs \(\alpha = 0,8\) et \(\beta= 0,5\) données.