Propriétés de la fonction DTS
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
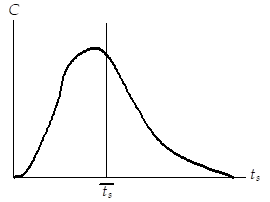
Considérons le signal mesuré en sortie du système, comme illustré sur la figure ci-contre.
Réponse à une impulsion : la fonction de distribution E
La \(E\) possède les propriétés usuelles des distributions. En particulier on peut définir les moments de cette distribution.
Définition : Moments de la distribution
Le moment d'ordre \(n\) de la fonction de distribution des temps de séjour est :
\(\mu_n = \int\limits_{0}^{\infty}{t_s^n \cdot E\ \left(t_s \right) \cdot \mathrm{d}t_s}\)
Le moment d'ordre 0, est le facteur de normation. Il est unitaire puisque \(E\ (t_s) = \frac{C\ (t_s)}{\int\limits_0^{\infty}{C\ (t) \cdot \mathrm{d}t}}\) :
\(\mu_0 = 1\)
Le moment d'ordre 1 représente la moyenne de la distribution. Il est relié au temps de séjour moyen \(\overline{t_s}\) par :
\(\overline{t_s} = \frac{\mu_1}{\mu0} = \mu_1\)
Le moment d'ordre 2 représente l'étalement autour du temps de séjour moyen. Il est lié à la variance \(\sigma^2\) par :
\(\sigma^2 = \frac{\mu_2}{\mu_0} - \left( \frac{\mu_1}{\mu_0} \right)^2 = \mu_2 - \mu_1^2\)
Le moment d'ordre 3 représente l'asymétrie de la distribution et le moment d'ordre 4 son aplatissement.
Remarque : Réponse à un échelon : la fonction F
La fonction \(F\) est simplement l'intégrale de la fonction de distribution des temps de séjour \(E\), elle apporte donc la même information. La méthode de mesure de la DTS[3] par injection échelon est donc dite "méthode intégrale".
\(F\ (t_s) = \int\limits_{0}^{t_s}{E\ (t) \cdot \mathrm{d}t}\)
Ceci se retrouve simplement en se rappelant que l'impulsion est la fonction dérivée de l'échelon.
Complément : Méthode à 2 points de mesure
Il est souvent difficile de réaliser pratiquement l'injection "proprement", en particulier d'avoir un temps d'injection très faible. Il peut également arriver que l'entrée du système que l'on souhaite étudier ne soit pas accessible, pour des raisons de sécurité par exemple.
La méthode dite des "deux points de mesure" permet, à partir d'une injection de forme quelconque, de déduire la DTS à l'aide de 2 mesures réalisées en entrée et en sortie du système comme illustré sur la figure suivante.
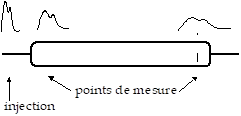
Le dépouillement s'effectue alors à partir des concentrations \(C^e\ \left( t_s \right)\) et \(C^s\ \left( t_s \right)\) mesurées en entrée et en sortie, à l'aide du produit de convolution :
\(C^s \ \left( t_s \right) = \int\limits_{0}^{t_s}{C^e\ (t) \cdot E\ \left( t_s - t \right) \cdot \mathrm{d}t}\)