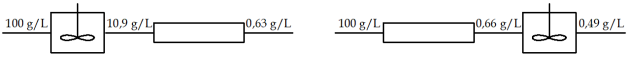Génie de la Réaction Chimique : les réacteurs homogènes

Le temps de séjour moyen est donné par : \(\overline{{{t}_{s}}}=\frac{{{\mu }_{1}}}{{{\mu }_{0}}}=\frac{\int\limits_{0}^{\infty }{{{t}_{s}}^{1}\cdot E\left( {{t}_{s}} \right)\cdot d{{t}_{s}}}}{\int\limits_{0}^{\infty }{{{t}_{s}}^{0}\cdot E\left( {{t}_{s}} \right)\cdot d{{t}_{s}}}}=\frac{\int\limits_{0}^{\infty }{{{t}_{s}}\cdot C\left( {{t}_{s}} \right)\cdot d{{t}_{s}}}}{\int\limits_{0}^{\infty }{C\left( {{t}_{s}} \right)\cdot d{{t}_{s}}}}\).

Pour le calculer à partir des mesures du tableau : \(\overline{{{t}_{s}}}=\frac{\sum\limits_{i}{{{t}_{i}}\cdot {{C}_{i}}\cdot \Delta t}}{\sum\limits_{i}{{{C}_{i}}\cdot \Delta t}}=\frac{\sum\limits_{i}{{{t}_{i}}\cdot {{C}_{i}}}}{\sum\limits_{i}{{{C}_{i}}}}\) = 22,5 minutes

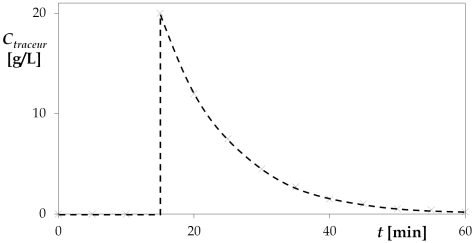
On remarque un retard pur (représentable par un réacteur piston) puis une décroissance exponentielle typique d'un RPA. Il est donc logique d'imaginer un modèle les associant en série.

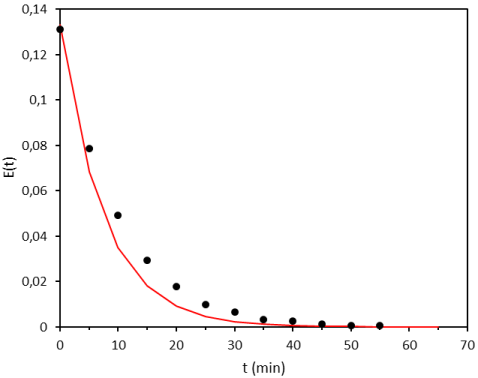
La distribution des temps de séjour pour un réacteur piston est \(C\left( {{t}_{s}} \right)={{C}_{0}}\cdot \delta \ \left( {{t}_{s}}-{{\tau }_{piston}} \right)\) ; pour un RPA, \(C={{C}_{0}}\cdot \exp \ \left( -\frac{{{t}_{s}}}{{{\tau }_{RPA}}} \right)\). La courbe C vs t tracée précédemment montre un retard pur de 15 min caractéristique d'un réacteur piston. Le temps de passage dans le RPA associé en série est donc de 7,5 minutes. La courbe en rouge sur le graphique suivant correspond au modèle de RPA avec ce temps de passage.

On supposera que \(\tau_{piston} =\) 15 min.

Le bilan en réactif sur le RPA s'écrit : \(Q\cdot {{C}^{{{e}_{RPA}}}}-k\cdot {{C}^{{{s}_{RPA}}}}^{2}\cdot {{V}_{RPA}}=Q\cdot {{C}^{{{s}_{RPA}}}}\).

Soit \(k\cdot {{\tau }_{RPA}}\cdot {{C}^{{{s}_{RPA}}}}^{2}+{{C}^{{{s}_{RPA}}}}-{{C}^{{{e}_{RPA}}}}=0\), qui est un polynôme du second degré en C_s

\({{C}^{{{s}_{RPA}}}}=\frac{\sqrt{1+4\cdot k\cdot {{\tau }_{RPA}}\cdot {{C}^{{{e}_{RPA}}}}}-1}{2\cdot k\cdot {{\tau }_{RPA}}}\) est la seule racine acceptable.

Le bilan en réactif sur le réacteur piston s'écrit : \(Q\cdot dC=-k\cdot {{C}^{2}}\cdot dV\)

Que l'on intègre : \(\int\limits_{{{C}^{{{e}_{piston}}}}}^{{{C}^{{{s}_{piston}}}}}{-\frac{dC}{{{C}^{2}}}}=\frac{k}{Q}\cdot \int\limits_{0}^{{{V}_{piston}}}{dV}\), soit \(\frac{1}{{{C}^{{{s}_{piston}}}}}-\frac{1}{{{C}^{{{e}_{piston}}}}}=k\cdot \frac{{{V}_{piston}}}{Q}=k\cdot {{\tau }_{piston}}\)

Finalement, \({{C}^{{{s}_{piston}}}}=\frac{{{C}^{{{e}_{piston}}}}}{1+k\cdot {{\tau }_{piston}}\cdot {{C}^{{{e}_{piston}}}}}\)

La seconde disposition est nettement plus favorable à la conversion, mais la DTS reste inchangée.

La fonction DTS est donnée par : \(E\ ({{t}_{s}})=\frac{C\ ({{t}_{s}})}{\int\limits_{0}^{\infty }{C\left( t \right)\cdot dt}}\). Avec \(\int\limits_{0}^{\infty }{C\left( t \right)\cdot dt}\approx \sum\limits_{i}{{{C}_{i}}\cdot \Delta t}=\)252,5 g min L^-1.

D'où le tableau :

Le produit de convolution est : \({{C}^{s}}\ \left( {{t}_{s}} \right)=\int\limits_{0}^{{{t}_{s}}}{{{C}^{e}}\ \left( t \right)\cdot E\ \left( {{t}_{s}}-t \right)\cdot dt}\)

D'où le tableau :

Enfin on vérifie que les aires sous-tendues à chaque courbe (proportionnelles à la quantité de traceur injecté) sont égales : \(\sum\limits_{i}{C_{i}^{e}}\) = 60 g/L = \(\sum\limits_{i}{C_{i}^{s}}\).