Réaction d'ordre 1 dans un RPA fermé uniforme

On met en œuvre la réaction en phase liquide A → P (d'ordre 1 par rapport au réactif A : \(r=k\cdot C_A\), avec \(k =\) 0,5 min-1) dans un réacteur fermé uniforme (contenant initialement 5 m3 d'une solution de A dans un solvant inerte, avec une concentration \(C_{A0} =\) 3 mol L-1).

Question

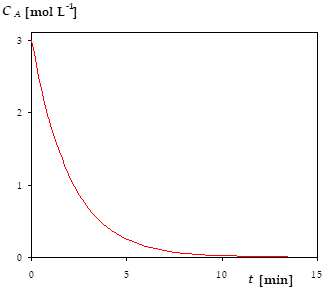
Comment évolue la concentration en réactif A en fonction du temps ?

Résultat

Concentration de A en fonction du tempsInformations[1]

Solution

La réaction ayant lieu en phase liquide, on suppose que le volume du milieu réactionnel peut être considéré comme constant. Par conséquent, \(-r = -k \cdot C_A = \frac{\mathrm{d} C_A}{\mathrm{d} t}\), soit \(\frac{\mathrm{d} C_A}{C_A} = -k \cdot \mathrm{d} t\). Donc \(\ln \ C_A = -k \cdot t + cste\). Comme à l'instant initial (\(t = 0\)), \(C_A=C_{A0}\), on a \(C_A = C_{A0} \cdot \exp \ \left( -k\cdot t \right)\). La concentration en réactif A évolue donc en fonction du temps comme une exponentielle décroissante.

On remarque que l'évolution de la composition du milieu ne dépend pas de son volume.

Concentration de A en fonction du tempsInformations[1]

Question

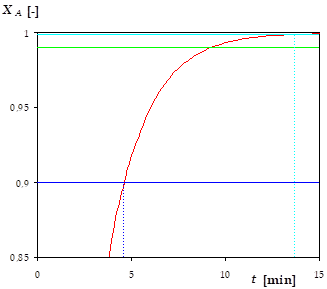
Combien de temps faut-il pour atteindre un taux de conversion de A de 90% ? de 99% ? de 99,9% ?

Résultat

4,6 min pour obtenir 90% de conversion de A

9,2 min pour avoir 99%

13,8 min pur 99,9%

Solution

Cela revient à rechercher les temps pour lesquels \(C_A/C_{A0}\) vaut 0,1 ; 0,01 ; 0,001. La relation précédente donne \(t=-\frac{1}{k} \cdot \ln \ \left( C_A/C_{A0} \right)\).

On atteint donc

  • 90% de conversion de A en 4,6 min ;

  • 99% en 9,2 min ;

  • 99,9% en 13,8 min.

Taux de conversion de A en fonction du tempsInformations[2]

Question

Reprise de toutes les questions en vidéo.

Solution en vidéo

GRC - exercice d'application : réacteur parfaitement agité fermé
Informations[3]