Fabrication de l'acétate d'éthyle (réaction équilibrée)
On veut réaliser à 100°C dans des conditions isothermes, l'estérification de l'acide acétique par l'alcool éthylique en acétate d'éthyle, à partir de 1 m3 de solution aqueuse, de masse volumique 1030 kg/m3 contenant 250 kg d'acide acétique, 500 kg d'alcool et 40 kg d'acide chlorhydrique (catalyseur).
La vitesse nette \(r\) est la différence entre la vitesse de l'estérification \(r_1\) et la vitesse de la réaction inverse \(r_2\). Ces vitesses sont exprimées par les relations suivantes :
\(r_1 = k_1 \cdot C_{AcAc} \cdot C_{EtOH}\) avec \(k_1 =\) 4,8 10-4 L mol-1 min-1
\(r_2 = k_2 \cdot C_{AcOEt} \cdot C_{H_2O}\) avec \(k_2 =\) 1,6 10-4 L mol-1 min-1
Question
En supposant qu'il n'y ait pas d'évaporation des réactifs ni des produits et que la masse volumique reste constante pendant tout le processus, déterminer le taux de conversion à l'équilibre et en fonction du temps.
Note : cet exercice demande pas mal de travail, mais en suivant les étapes données par les indices, vous devriez être en mesure de le réaliser ; persévérez dans vos tentatives avant de regarder la solution !
Indice
Commencer par expliciter la vitesse nette \(r = r_1 - r_2\) en fonction du taux de conversion en acide acétique (que l'on pourra noter \(X_A\)).
Indice
Écrire qu'à l'équilibre, \(r = 0\). On obtient alors un polynôme du second degré, dont la seule racine comprise entre 0 et 1 correspond à \(X_A^{eq}\), que l'on peut calculer.
Indice
Calculer le taux de conversion en fonction du temps :
soit par intégration numérique (méthode des trapèzes) ;
soit à partir de la forme factorisée du polynôme du second degré (en faisant intervenir \(X_A^{eq}\) et la seconde racine (non comprise entre 0 et 1) que l'on pourra noter \(Z\).)
Solution
Le taux de conversion à l'équilibre vaut 61%.
Solution
La réaction s'écrit : CH3COOH + C2H5OH → CH3COOC2H5 + H2O
ou en version abrégée : AcAc(A) + EtOH → AcOEt + H2O
La vitesse nette est : \(r={{k}_{1}}\cdot C_{AcAc} \cdot C_{EtOH} - k_2 \cdot C_{AcOEt} \cdot C_{H_2O}\).
Initialement, le réacteur contient :
250 kg d'acide acétique (\(M_{AcAc} =\) 60 g/mol) soit 4167 mol d'AcAc ;
500 kg d'alcool (\(M_{EtOH} =\) 46 g/mol), soit 10 870 mol d'EtOH ;
1030-250-500-40 kg d'eau (\(M_{H_2O}\) = 18 g/mol), soit 13 333 mol d'H2O ;
pas d'acétate d'éthyle, soit 0 mol d'AcOEt ;
pour un total de \(V_0 =\) 1 m3.
L'acide acétique est donc le réactif clé, dont on définit le taux de conversion : \(n_A = n_{A,0} \cdot \left( 1-X_A \right)\)
À l'équilibre, \(r = 0\), soit
\(k_1 \cdot \frac{n_{AcAc,0} \cdot \left( 1-X_{A,eq} \right)}{V_{0}} \cdot \frac{n_{EtOH,0} - n_{AcAc,0} \cdot X_A^{eq}}{V_0} = k_2 \cdot \frac{n_{AcAc,0} \cdot X_A^{eq}}{V_0} \cdot \frac{n_{H2O,0} + n_{AcAc,0} \cdot X_A^{eq}}{V_0}\)
Que l'on peut réarranger en : \(\left( k_1 -k_2 \right) \cdot n_{AcAc,0} \cdot {X_A^{eq}}^2 - \left[ k_1 \cdot \left( n_{AcAc,0} + n_{EtOH,0} \right) + k_2 \cdot n_{H2O,0} \right] \cdot X_A^{eq} + k_1 \cdot n_{EtOH,0} = 0\)
Ce polynôme du second degré (\(a \cdot {X_A^{eq}}^2 + b \cdot X_A^{eq} + c = 0\) ; \(a =\) 1,333 L/min ; \(b =\) 9,351 L/min ; \(c =\) 5,217 L/min) admet deux solutions, dont l'une seulement est comprise entre 0 et 1 : c'est \(X_A^{eq}\) ; l'autre solution sera notée \(Z\) :
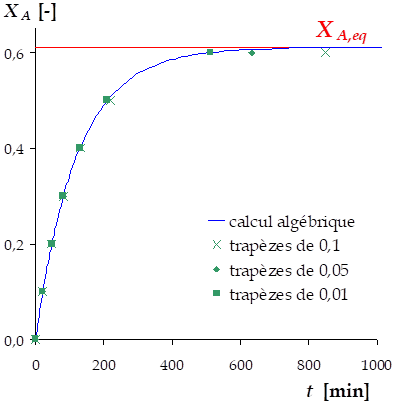
\(X_A^{eq} =\frac{-b-\sqrt{b^2 - 4 \cdot a \cdot c}}{2 \cdot a} =\) 0,6112 (valeur que l'on retrouve sur le graphique \(X_A\) vs \(t\))
\(Z = \frac{-b+\sqrt{b^2 - 4 \cdot a\cdot c}}{2 \cdot a} =\) 6,4018
Le taux de conversion maximum qui peut être atteint dans les conditions de travail est donc 61%.
Le bilan en acide acétique sur ce réacteur s'écrit : \(-r \cdot V = \frac{\mathrm{d} n_A}{\mathrm{d} t}\). Soit, puisque le volume est considéré comme constant (égal à \(V_0\)),
\(- n_{AcAc,0} \cdot \frac{\mathrm{d} X_A}{\mathrm{d} t} = -\left[ k_1 \cdot \frac{n_{AcAc,0} \cdot \left( 1-X_A \right)}{V_0} \cdot \frac{n_{EtOH,0}-n_{AcAc,0} \cdot X_A}{V_0} - k_2 \cdot \frac{n_{AcAc,0} \cdot X_A}{V_0} \cdot \frac{n_{H2O,0} + n_{AcAc,0} \cdot X_A}{V_0} \right] \cdot V_0\)
\(- n_{AcAc,0} \cdot \frac{\mathrm{d} X_A}{\mathrm{d} t} = - \frac{n_{AcAc,0}}{V_0} \cdot \left[ \left( k_1 -k_2 \right) \cdot n_{AcAc,0} \cdot {X_A^{eq}}^2 - \left[ k_1 \cdot \left( n_{AcAc,0} + n_{EtOH,0} \right) + k_2 \cdot n_{H2O,0} \right] \cdot X_A^{eq} + k_1 \cdot n_{EtOH,0} \right]\)
D'où : \(\frac{\mathrm{d} X_A}{\left( k_1 -k_2 \right) \cdot n_{AcAc,0} \cdot {X_A^{eq}}^2 - \left[ k_1 \cdot \left( n_{AcAc,0} + n_{EtOH,0} \right) + k_2 \cdot n_{H2O,0} \right] \cdot X_A^{eq} + k_1 \cdot n_{EtOH,0}} = \frac{\mathrm{d} t}{V_0}\)
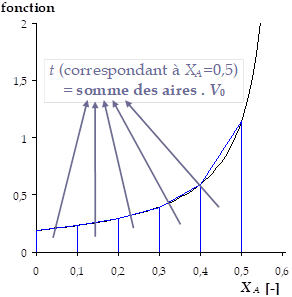
Cette équation peut être intégrée numériquement, par exemple par la méthode des trapèzes. Cela revient à tracer la fonction \(\frac{1}{\left( k_1 -k_2 \right) \cdot n_{AcAc,0} \cdot {X_A^{eq}}^2 - \left[ k_1 \cdot \left( n_{AcAc,0} + n_{EtOH,0} \right) + k_2 \cdot n_{H2O,0} \right] \cdot X_A^{eq} + k_1 \cdot n_{EtOH,0}}\) en fonction de \(X_A\) et à estimer l'aire sous-tendue à la courbe pour chaque valeur de \(X_A\), afin d'en déduire le temps \(t\) correspondant, comme illustré sur le graphique suivant.
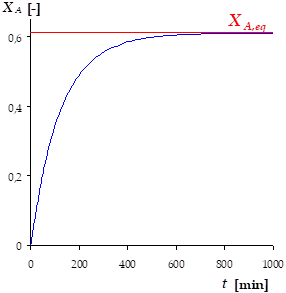
En répétant l'opération pour diverses valeurs de \(X_A\), on obtient la courbe \(X_A\) vs \(t\) :

Ces calculs peuvent être effectués à l'aide d'un tableur ou d'un programme.
On peut aussi remarquer que, à l'aide des solutions du polynôme du second degré trouvées précédemment, l'équation peut se mettre sous la forme : \(\frac{\mathrm{d} X_A}{\left( k_1 - k_2 \right) \cdot n_{AcAc,0} \cdot \left( X_A -X_A^{eq} \right) \cdot \left( X_A - Z \right)} = \frac{\mathrm{d} t}{V_0}\)
Or on peut mettre \(\frac{1}{\left( x - x_1 \right)\cdot \left( x - x_2\right)}\) sous la forme \(\frac{\alpha}{x - x_1} + \frac{\beta}{x - x_2}\)
En effet \(\frac{\alpha}{x - x_1}+\frac{\beta}{x - x_2}=\frac{\alpha \cdot \left( x - x_2 \right) +\beta \cdot \left( x - x_1 \right)}{\left( x - x_1 \right)\cdot \left( x - x_2 \right)} = \frac{\left( \alpha +\beta \right) \cdot x - \left( \alpha \cdot x_2+\beta \cdot x_1 \right)}{\left( x - x_1 \right) \cdot \left( x - x_2 \right)}\)
par identification, on voit qu'il faut que \(\alpha + \beta = 0\), donc \(\beta = -\alpha\), et \(-\left( \alpha \cdot x_2 +\beta \cdot x_1 \right) = 1= - \left( \alpha \cdot x_2 -\alpha \cdot x_1 \right)\), soit \(\alpha =\frac{1}{x_1 - x_2}\)
finalement : \(\frac{1}{\left( x - x_1 \right)\cdot \left( x - x_2 \right)} = \frac{1}{x_1 - x_2} \cdot \left[ \frac{1}{x - x_1} - \frac{1}{x - x_2} \right]\)
Soit, \(\frac{\mathrm{d} X_A}{\left( X_A - X_A^{eq} \right) \cdot \left( X_A - Z \right)} = \frac{1}{Z - X_A^{eq}} \cdot \left( \frac{\mathrm{d} X_A}{X_A - Z} - \frac{\mathrm{d} X_A}{X_A - X_A^{eq}} \right) = \frac{\left( k_1 - k_2 \right) \cdot n_{AcAc,0}}{V_0} \cdot \mathrm{d} t\)
Que l'on peut intégrer : \(\ln \ \left( \frac{X_A -Z}{-Z} \right) - \ln \ \left( \frac{X_A - X_A^{eq}}{-X_A^{eq}} \right) = \frac{\left( k_1 - k_2 \right) \cdot n_{AcAc,0}}{V_0} \cdot \left( Z - X_A^{eq} \right) \cdot t\)
Soit, \(\ln \ \left( \frac{X_A - Z}{X_A - X_A^{eq}} \cdot \frac{X_A^{eq}}{Z} \right) = \frac{\left( k_1 - k_2 \right) \cdot n_{AcAc,0}}{V_0} \cdot \left( Z - X_A^{eq} \right) \cdot t\)
On peut alors calculer \(t\) pour diverses valeurs de \(X_A\) et comparer avec la méthode numérique :