Gradients de température
Généralement, \(T_s - T_e >> (T - T_s)_{max}\) en phase gazeuse : le gradient de température se situe essentiellement dans le film gazeux autour du grain de catalyseur.
Au contraire, dans les systèmes liquide/solide, le gradient de température est plutôt localisé dans le grain.
Remarque :
Le gradient de température externe maximal est \((T_s - T_e)_{max} = \frac {k \cdot C_e \cdot (- \Delta rH)}{h}\) ; il dépend notamment des conductances de transfert externe de matière \(k\)[1] et thermique \(h\)[2], ainsi que de la concentration \(C_e\) loin du grain de catalyseur.
Le gradient de température interne maximal est \((T - T_s)_{max} = \beta \cdot T_s = \frac {D_e \cdot C_s \cdot (- \Delta rH)}{\lambda_e}\) ; il dépend notamment des diffusivités effectives de matière \(D_e\)[3] et thermique \(\lambda_e\)[4], ainsi que de la concentration \(C_s\) en surface du grain de catalyseur.
Notion fondamentale :
La figure suivante fournit le facteur d'efficacité en fonction de \(\phi_s = L \cdot \sqrt{ \frac{k}{D_e} }\) (qui vaut \(\sqrt{ {\varphi_s}^2}\) pour une cinétique d'ordre 1) pour diverses valeurs du critère de thermicité \(\beta\)[5] et pour une valeur donnée du critère d'activation \(\gamma\)[6].
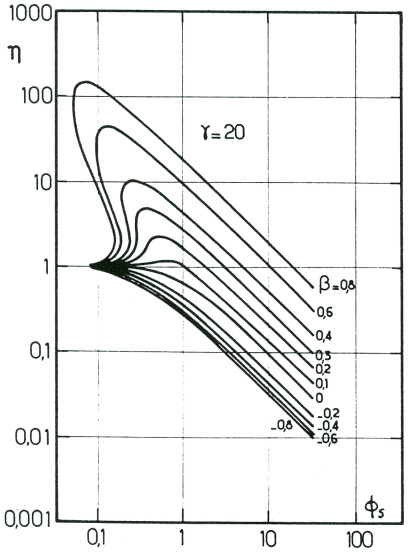
Pour une valeur de \(\phi_s\) donnée, on peut avoir jusqu'à trois points de fonctionnement possibles, dont deux sont stables (un froid et un chaud). C'est une situation rare industriellement ; qui peut arriver en cas de réaction fortement exothermique.
La surchauffe interne du grain compense la faible concentration et la vitesse de réaction reste conséquente : le facteur d'efficacité est alors très grand.