Réaction isotherme du premier ordre sans limitation par le transfert externe
Raisonnement :
En isotherme, \(\beta = 0\) et \(\theta = 1\).
En l'absence de limitation par le transfert externe, le nombre de BIOT matière est infini.
Si la réaction est d'ordre 1, \(n = 1\).
Le système d'équations différentielles se limite alors à celle du bilan matière avec ses conditions limites :
\(\left\{ \begin{array} {c} \frac{\mathrm{d}^2 \mathbb{C}}{\mathrm{d} x^2} = \varphi_s \cdot \mathbb{C} \\ \mathbb{C} = 1 \mathrm{en \:} x=0 \\ \left( \frac{\mathrm{d} \mathbb{C}}{\mathrm{d} x} \right) _{x=1} = 0\end{array} \right.\)
La solution de cette équation différentielle est de la forme : \(\mathbb{C} = a_1 \cdot \exp \left( \varphi_s \cdot x \right) + a_2 \cdot \exp \left( - \varphi_s \cdot x \right)\), où \(a_1\) et \(a_2\) peuvent être obtenues grâce aux conditions limites.
Remarque :
Par définition, \(\overline{r} = \frac{1}{L} \cdot \int_0^L r(C,T) \cdot \mathrm{d} z = \eta_s \cdot r_s\).
Or en isotherme \(T = T_s\), donc \(\overline{r} = \frac{1}{L} \cdot \int_0^L k_0 \cdot \exp \left( \frac{-E_a}{\mathcal{R} \cdot T_s} \right) \cdot C \cdot \mathrm{d} z = k_0 \cdot \exp \left( \frac{-E_a}{\mathcal{R} \cdot T_s} \right) \cdot C_s \cdot \int_0^1 \mathbb{C} \cdot \mathrm{d} x = r_s \cdot \int_0^1 \mathbb{C} \cdot \mathrm{d} x \). Par identification, il vient \(\eta_s = \int_0^1 \mathbb{C} \cdot \mathrm{d} x\).
Notion fondamentale :
Compte tenu de la forme de la solution \(\mathbb{C}\) de l'équation différentielle,
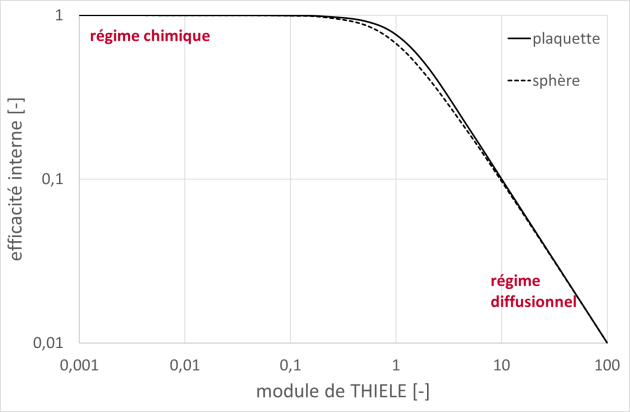
Lorsque \({\varphi_s}^2 << 1\), \(\mathbb{C} = 1\) et \(\eta_s = 1\), c'est le régime chimique[2] (la concentration en réactif fluide est la même dans les pores du catalyseur et loin des grains de catalyseur et la vitesse du processus est imposé par la cinétique chimique).
Lorsque \({\varphi_s}^2 >> 1\), \(\mathbb{C} = \exp \left( - \varphi_s \cdot x \right)\) et \(\eta_s = \frac{1}{\varphi_s}\), c'est le régime diffusionnel[3] (la réaction est rapide par rapport à la diffusion, qui impose sa vitesse au processus global).
La courbe facteur d'efficacité vs module de THIELE a l'allure suivante.
La forme de la courbe dans la zone de régime intermédiaire (où il n'y a prédominance ni de la cinétique chimique ni du transfert par diffusion) dépend de la forme des grains de catalyseurs. Ainsi pour des grains sphériques, la solution de l'équation différentielle du bilan matière fournit : \(\eta_s = \frac{3 \cdot \varphi_s \cdot \mathrm{coth \:} (3 \cdot \varphi_s ) - 1}{3 \cdot {\varphi_s}^2}\) et la courbe se trouve un peu en dessous de celle représentée ci-dessus. En revanche les asymptotes en régimes chimique et diffusionnel sont inchangées.
On considère généralement le régime intermédiaire (mixte) pour \(0,3 < \varphi_s < 3\).
Exemple :
Pour des grains d'autres formes, la longueur caractéristique \(L = \frac{V_p}{A_p}\) (où \(V_p\) est le volume de la particule de catalyseur et \(A_p\) sa surface) prend diverses expressions (\(\frac{R}{2}\) pour un cylindre allongé ; \(\frac{R}{3}\) pour une sphère), mais on a toujours :
\(\eta_s \rightarrow 1\) lorsque \({\varphi_s}^2 << 1\) : régime chimique,
\(\eta_s \rightarrow \frac{1}{\varphi_s}\) lorsque \({\varphi_s}^2 >> 1\) : régime diffusionnel.
L'inconvénient du module de THIELE défini précédemment est qu'il dépend de grandeurs difficilement accessibles (\(C_s\) et \(T_s\) : en surface du grain de catalyseur). On définit donc des critères modifiés (ou observables).
Définition : critères de THIELE modifiés (ou observables)
On définit des critères de THIELE modifiés observables : \(\varphi_s' = \frac{ \overline{r} \cdot L^2}{D_e \cdot C_s}\) et \(\varphi_e' = \frac{ \overline{r} \cdot L^2}{D_e \cdot C_e}\).
Le premier, défini par rapport aux conditions de surface, est appelé critère de WEISZ[5]. Pour une cinétique de réaction d'ordre \(n\) quelconque, il s'écrit : \(\varphi_s' = \frac{n+1}{2} \cdot \frac{ \overline{r} \cdot L^2}{D_e \cdot C_s}\)
Remarque :
Les frontières des régimes demeurent pour les mêmes valeurs (0,3 et 3).