Modélisation de la diffusion dans une plaquette de catalyseur
Raisonnement :
La loi de FICK fournit la densité de flux de \(A\) qui diffuse à travers un plan parallèle à la surface de la particule : \(J = -D_e \cdot \frac{\mathrm{d} C}{\mathrm{d} z}\).
Le bilan sur une tranche de particule d'épaisseur \(\mathrm{d} z\) s'écrira donc :
\(- \Omega \cdot D_e \cdot \frac{\mathrm{d} C}{\mathrm{d} z} - r \cdot \Omega \cdot \mathrm{d}z = - \Omega \cdot D_e \cdot \left( \frac{\mathrm{d} C}{\mathrm{d} z} + \frac{\mathrm{d}^2 C}{\mathrm{d} z^2} \cdot \mathrm{d}z \right)\)
Il vient alors \(D_e \cdot \frac{\mathrm{d}^2 C}{\mathrm{d} z^2} = r\).
De la même manière, le bilan thermique fournit \(\lambda_e \cdot \frac{\mathrm{d}^2 T}{\mathrm{d} z^2} = r \cdot \Delta rH\).
Les conditions limites à la surface du grain sont :
\(-D_e \cdot \frac{\mathrm{d} C}{\mathrm{d} z} = k \cdot \left( C_e - C_s \right)\) en \(z = 0\) pour le transfert de matière ;
\(-\lambda_e \cdot \frac{\mathrm{d} T}{\mathrm{d} z} = h \cdot \left( T_e - T_s \right)\) en \(z = 0\) pour le transfert thermique.
Ceci traduit la continuité des flux internes et externes.
On a bien sûr les mêmes égalité en \(z = 2 \cdot L\).
Pour raison de symétrie, au centre de la plaquette de catalyseur (en \(z = L\)), \(\frac{\mathrm{d} C}{\mathrm{d} z} = 0\) et \(\frac{\mathrm{d} T}{\mathrm{d} z} = 0\).
Supposons pour faire au plus simple, que la vitesse de réaction puisse s'écrire sous la forme d'un ordre \(n\) avec une loi d'ARRHENIUS : \(r = k_0 \cdot \exp \left( \frac{-E_a}{\mathcal{R} \cdot T} \right) \cdot C^n\).
Raisonnement :
On définit les grandeurs réduites : \(\mathbb{C} = \frac{C}{C_s}\) ; \(\theta = \frac{T}{T_s}\) ; \(x = \frac{z}{L}\).
On peut alors réécrire les équations précédentes :
bilan de matière : \(D_e \cdot \frac{C_s}{L^2} \cdot \frac{\mathrm{d}^2 \mathbb{C}}{\mathrm{d} x^2} = r = k_0 \cdot \exp \left( \frac{-E_a}{\mathcal{R} \cdot \theta \cdot T_s} \right) \cdot {C_s}^n \cdot {\mathbb{C}}^n\) ;
bilan thermique : \(\lambda_e \cdot \frac{T_s}{L^2} \cdot \frac{\mathrm{d}^2 \theta}{\mathrm{d} x^2} = r \cdot \Delta rH\) ;
conditions limites :
\(-D_e \cdot \frac{C_s}{L} \cdot \left( \frac{\mathrm{d} \mathbb{C}}{\mathrm{d} x} \right) _{x=0} = k \cdot C_s \cdot \left( \mathbb{C}_e - 1 \right)\) pour la continuité du transfert de matière en surface du grain de catalyseur,
\(-\lambda_e \cdot \frac{T_s}{L} \cdot \left( \frac{\mathrm{d} \theta}{\mathrm{d} x} \right) _{x=0} = h \cdot T_s \cdot \left( \theta_e - 1 \right)\) pour la continuité du transfert thermique en surface du grain de catalyseur,
\(\left( \frac{\mathrm{d} \mathbb{C}}{\mathrm{d} x} \right) _{x=1} = 0\) et \(\left( \frac{\mathrm{d} \theta}{\mathrm{d} x} \right) _{x=1} = 0\) pour les conditions de symétrie.
Remarque :
\(r_s = k_0 \cdot \exp \left( \frac{-E_a}{\mathcal{R} \cdot T_s} \right) \cdot {C_s}^n\) est la vitesse dans les conditions en surface du grain[1] \(\left( C_s,T_s \right)\).
On peut de la même façon définir \(r_e = k_0 \cdot \exp \left( \frac{-E_a}{\mathcal{R} \cdot T_e} \right) \cdot {C_e}^n\) : vitesse dans les conditions loin du grain[2] \(\left( C_e,T_e \right)\).
Raisonnement :
Le bilan matière peut s'écrire : \(\frac{\mathrm{d}^2 \mathbb{C}}{\mathrm{d} x^2} = \frac{L^2}{D_e \cdot C_s} \cdot k_0 \cdot \exp \left( \frac{-E_a}{\mathcal{R} \cdot \theta \cdot T_s} \right) \cdot {C_s}^n \cdot {\mathbb{C}}^n \cdot \exp \left( \frac{-E_a}{\mathcal{R} \cdot T_s} \right) \cdot \exp \left( \frac{E_a}{\mathcal{R} \cdot T_s} \right)\) pour faire apparaître \(r_s\) et ainsi obtenir : \(\frac{\mathrm{d}^2 \mathbb{C}}{\mathrm{d} x^2} = \frac{L^2}{D_e \cdot C_s} \cdot r_s \cdot \exp \left( \frac{-E_a}{\mathcal{R} \cdot \theta \cdot T_s} + \frac{E_a}{\mathcal{R} \cdot T_s} \right) \cdot {\mathbb{C}}^n\) que l'on réarrange en \(\frac{\mathrm{d}^2 \mathbb{C}}{\mathrm{d} x^2} = \frac{L^2}{D_e \cdot C_s} \cdot r_s \cdot \exp \left[ \frac{-E_a}{\mathcal{R} \cdot T_s} \cdot \left( \frac{1}{\theta} -1 \right) \right] \cdot {\mathbb{C}}^n\)
La condition de continuité sur le transfert de matière s'écrit : \(\left( \frac{\mathrm{d} \mathbb{C}}{\mathrm{d} x} \right) _{x=0} = \frac{k \cdot L}{D_e} \cdot \left(1 - \mathbb{C}_e \right)\).
Définition : module de THIELE, critère d'activation et nombre de BIOT matière
On nomme critère (ou module) de THIELE \({\varphi_s}^2\)[3] = \(\frac{L^2}{D_e \cdot C_s} \cdot r_s\) et critère d'activation \(\gamma\)[4] = \(\frac{E_a}{\mathcal{R} \cdot T_s}\).
\(\frac{k \cdot L}{D_e}\) n'est autre que le nombre de BIOT matière \({Bi}_M\)[5].
Raisonnement :
Le bilan matière devient donc : \(\frac{\mathrm{d}^2 \mathbb{C}}{\mathrm{d} x^2} ={\varphi_s}^2 \cdot \exp \left(- \gamma \cdot \frac{1-\theta}{\theta} \right) \cdot {\mathbb{C}}^n\)
Le bilan thermique peut quant à lui s'écrire : \(\frac{\mathrm{d}^2 \theta}{\mathrm{d} x^2} = - \beta \cdot {\varphi_s}^2 \cdot \exp \left(- \gamma \cdot \frac{1-\theta}{\theta} \right) \cdot {\mathbb{C}}^n\)
Définition : critère de thermicité
Où le critère de thermicité de PRATER \(\beta\)[6] = \(\frac{D_e \cdot C_s \cdot (_\Delta rH)}{\lambda_e \cdot T_s}\) correspond au gradient maximum de température réduite \(\left( \frac{T - T_s}{T_s} \right)_{maxi}\).
Raisonnement :
Les conditions limites quant à elles peuvent s'écrire :
\(\left( \frac{\mathrm{d} \mathbb{C}}{\mathrm{d} x} \right) _{x=0} = Bi_M \cdot \left(1 - \mathbb{C}_e \right)\) pour la continuité du transfert de matière en surface du grain de catalyseur,
\(\left( \frac{\mathrm{d} \theta}{\mathrm{d} x} \right) _{x=0} = Bi_T \cdot \left(1 - \theta_e \right)\) pour la continuité du transfert thermique en surface du grain de catalyseur,
\(\left( \frac{\mathrm{d} \mathbb{C}}{\mathrm{d} x} \right) _{x=1} = 0 = \left( \frac{\mathrm{d} \theta}{\mathrm{d} x} \right) _{x=1}\) pour les conditions de symétrie.
Définition : nombre de BIOT thermique
Avec le nombre de BIOT thermique \({Bi}_T\)[7] = \(\frac{h \cdot L}{\lambda_e}\).
Méthode :
Le système d'équations obtenu (2 équations différentielles correspondant aux bilans + 4 conditions limites) ne peut être résolu que numériquement dans le cas général.
Dans certaines conditions particulières, le système peut être résolu algébriquement. Nous verrons un cas dans la suite.
Notion fondamentale :
Les valeurs des différents critères déterminent le régime réactionnel du grain de catalyseur ; ainsi que les formes des profils de concentration et de température au sein du grain illustrées sur la figure ci-dessous.
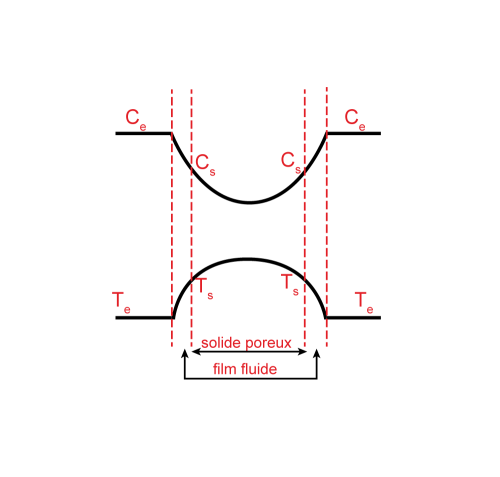
À noter que la pente des profils de concentration ou de température sont -dans le cas général- différentes dans le film fluide d'une part et dans le grain de catalyseur à proximité de la surface d'autre part.
Notion fondamentale :
Rappelons l'ensemble des critères adimensionnels définis :
La vitesse apparente moyenne[9] est \(\overline{r} = \frac{1}{V_p} \cdot \int_{V_p} r(C,T) \cdot \mathrm{d} V_p\) (où \(V_p\) est le volume de la particule de catalyseur) ; \(\overline{r} = \frac{1}{L} \cdot \int_0^L r(C,T) \cdot \mathrm{d} z\) pour notre particule feuillet.
Définition : facteurs d'efficacité
Les facteurs d'efficacité \(\eta_s\)[10] et \(\eta_e\)[11] sont tels que \(\overline{r} = r_s \cdot \eta_s = r_e \cdot \eta_e\), où \(r_s\)[1] et \(r_e\)[2] sont les vitesses respectivement dans les conditions de surface et loin du grain.