Réaction autocatalytique en phase liquide : comparaison de performance de réacteurs idéaux

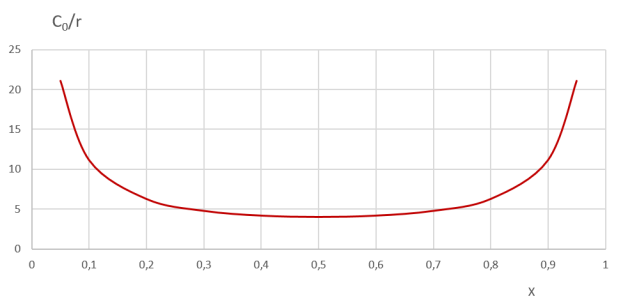
On étudie une réaction autocatalytique de la forme A + B = B + B en phase liquide. La vitesse est d'ordre 1 en A et 1 en B ; la constante de vitesse est de 1 L mol-1 min-1. On désire traiter une solution contenant A (\(C_{A0} =\) 0,99 mol L-1) et un peu de B (\(C_{B0} =\) 0,01 mol L-1) et on veut la convertir de façon à obtenir une solution contenant \(C_A =\) 0,1 mol L-1 et \(C_B =\) 0,9 mol L-1.

On prendra comme référence \(C_0 =\) 1 mol L-1, si bien que les concentrations pourront s'écrire sous la forme \(C_A = C_0 \cdot (1-X)\) et \(C_B = C_0 \cdot X\), avec \(X^E =\) 0,01 et \(X^S =\) 0,9.

Informations[1]

Question

  1. Calculer le temps de passage d'un réacteur parfaitement agité unique et isotherme.

  2. Le comparer à celui d'un réacteur piston, isotherme également.

  3. Proposer un arrangement de réacteur idéaux permettant de minimiser le temps de passage. Calculer le temps de passage dans chacun des réacteurs idéaux, ainsi que le temps de passage global.

On envisage de traiter un liquide contenant seulement A (\(C_{A0} =\) 1 mol L-1) et pas de B. On pourra toujours écrire \(C_A = C_0 \cdot (1-X)\) et \(C_B = C_0 \cdot X\).

On vise toujours \(X^S =\) 90%.

4. Quel dispositif permet alors de mettre en œuvre cette réaction ?

5. Calculer son temps de passage pour un taux de recyclage \(R = 1\) ?

6. Trouver la valeur du taux de recyclage permettant de minimiser le temps de passage d'un réacteur piston à recyclage ?

Résultat

  1. \(\tau_{RPA} =\) 9,9 min

  2. \(\tau_{piston} =\) 6,8 min

  3. 1 RPAC jusque \(X_1 =\) 0,5 puis 1 RP de \(X_1 =\) 0,5 à \(X^S =\) 0,9 : \(\tau_{RPAC} =\) 1,96 min + \(\tau_{RP} =\) 2,2 min

  4. Un réacteur piston avec recyclage.

  5. \(\tau_{piston \ recyclage} =\) 4,8 min

  6. \(R_{optimal} =\) 0,43

Solution en vidéo

Réaction autocatalytique en phase liquide : comparaison de performance de réacteurs idéaux
Informations[2]