Génie de la Réaction Chimique : les réacteurs homogènes

31 kg/h de E correspondent à 500 mol/h puisque \(M_E =\) 62 g/mol

Si l'on veut \(F_0 \cdot X =\) 500 mol/h avec \(X =\) 40%, il faut que \(F_0 = {500}/{0,4}\) mol/h.

On veut en outre une alimentation équimolaire en A et B, d'où \(F_{A1} = \frac{F_0}{2} =\) 625 mol/h \(= F_{B2}\)

D'où le débit volumique de solution 1 : \(Q_{v1} = F_{A1} \cdot \frac{M_A}{w_A \cdot \rho} = \frac{{500}/{0,4}}{2} \cdot \frac{0,0805}{0,322 \times 1} =\)156,25 L/h

De même pour le débit volumique de solution 2 : \(Q_{v2} = F_{B2} \cdot \frac{M_B}{w_B \cdot \rho} = \frac{{500}/{0,4}}{2} \cdot \frac{0,084}{0,168 \times 1} =\)312,5 L/h

Le bilan en A sur le RPA s'écrit : \(F_{A1} - r \cdot V_{RPA} = F_{A1} - F_0 \cdot X\)

Or la loi de vitesse est : \(r = k \cdot C_A \cdot C_B\), avec \(C_A = \frac{F_A}{Q_v}\) et \(C_B = \frac{F_B}{Q_v}\), où \(Q_v = Q_{v1} + Q_{v2} =\) 464 L/h (masse volumique constante).

D'où \(r = k \cdot \frac{\left( F_{A1} - F_0 \cdot X \right) \cdot \left( F_{B2} - F_0 \cdot X \right)}{Q_v^2} = k \cdot \frac{\left( {F_0}/{2} - F_0 \cdot X \right)^2}{Q_v^2}\) puisque \(F_{A1} = \frac{F_0}{2} = F_{B2}\).

Le bilan précédent devient donc : \({F_0}/{2} - k \cdot \frac{\left( {F_0}/{2} - F_0 \cdot X \right)^2}{Q_v^2} \cdot V_{RPA} = {F_0}/{2} - F_0 \cdot X\), d'où \(V_{RPA} = \frac{Q_v^2}{k \cdot F_0} \cdot \frac{X}{\left( {1}/{2} - X \right)^2} =\)1148 L

Le bilan en A sur une tranche de réacteur piston s'écrit : \(- r \cdot \mathrm{d}V = \mathrm{d}F_A = - F_0 \cdot \mathrm{d}X\)

Donc : \(k \cdot \frac{\left( {F_0}/{2} - F_0 \cdot X \right)^2}{Q_v^2} \cdot \mathrm{d}V = F_0 \cdot \mathrm{d}X\)

Donc \(\mathrm{d}V = \frac{F_0 \cdot Q_v^2}{k} \cdot \frac{\mathrm{d}X}{\left( {F_0}/{2} - F_0 \cdot X \right)^2}\)

Soit, \(V_{piston} = \frac{F_0 \cdot Q_v^2}{k} \cdot \int\limits_{0}^{X^s}{\frac{\mathrm{d}X}{\left( {F_0}/{2} - F_0 \cdot X \right)^2}} = - \frac{Q_v^2}{k} \cdot \int\limits_{0}^{X^s}{\frac{\mathrm{d} \left( {F_0}/{2} - F_0 \cdot X \right)}{\left( {F_0}/{2} - F_0 \cdot X \right)^2}} =\frac{Q_v^2}{k} \cdot \left[ \frac{1}{\left( {F_0}/{2} - F_0 \cdot X \right)} \right]_{0}^{X^s} = \frac{Q_v^2}{k} \cdot \left[ \frac{1}{ {F_0}/{2} - F_0 \cdot X^s} - \frac{1}{{F_0}/{2}} \right] = \frac{2 \cdot Q_v^2}{k \cdot F_0} \cdot \left[ \frac{1}{1 - 2 \cdot X^s} -1 \right] = \frac{2 \cdot Q_v^2}{k \cdot F_0} \cdot \frac{1 - 1 + 2 \cdot X^s}{1 - 2 \cdot X^s}\)

Finalement \(V_{piston} = \frac{4 \cdot Q_v^2}{k \cdot F_0} \cdot \frac{X^s}{1 - 2 \cdot X^s} =\)230 L

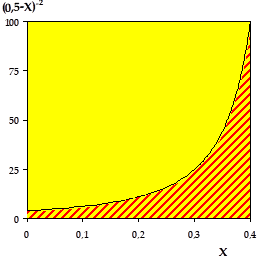
Le volume du RPA calculé est nettement supérieur à celui du réacteur piston, ce qui est tout à fait normal dans la mesure où \(\frac{1}{r} \propto \frac{1}{\left( {1}/{2} - X \right)^2}\) est une fonction croissante de \(X\) :

Sur le graphique suivant, l'aire en jaune est proportionnelle au volume du RPA ; l'aire hachurée de rouge est proportionnelle au volume du réacteur piston.