Génie de la Réaction Chimique : les réacteurs homogènes

16,7 m³

Le taux de conversion de A est tel que : \(F_A = F_{A0} \cdot \left( 1 - X_A \right)\), avec \(F_{A0} = a \cdot Q_v\). Si on considère que le débit volumique est constant, cela revient à : \(C_A = \frac{F_A}{Q_v} = a \cdot \left( 1 - X_A \right)\).

Et on a \(C_B = \frac{F_B}{Q_v} = b - a \cdot X_A\) et \(C_C = \frac{F_C}{Q_v} = c + a \cdot X_A\). Le vitesse de la réaction est donc : \(r = k \cdot a \cdot \left(1 - X_A \right) \cdot \left(c + a \cdot X_A \right)\)

Le bilan en A dans un RPA s'écrit : \(F_{A0} - r \cdot V_{RPA} = F_A\), soit \(a \cdot Q_v - k \cdot a \cdot \left( 1 - X_A^s \right) \cdot \left( c + a \cdot X_A \right) \cdot V_{RPA} = Q_v \cdot a \cdot \left( 1 - X_A^s \right)\).

D'où \(V_{RPA} = \frac{Q_v}{k} \cdot \frac{a \cdot X_A^s}{a \cdot \left( 1 - X_A^s \right) \cdot \left( c + a \cdot X_A^s \right)} =\)16,7 m³ (pour \(X_A^s =\)0,90)

9,4 m³

Le bilan en A dans un réacteur piston s'écrit : \(\mathrm{d}F_A = -r \cdot \mathrm{d}V\)

Soit \(-Q_v \cdot a \cdot \mathrm{d}X_A = - k \cdot a \cdot \left( 1 - X_A \right) \cdot \left( c + a \cdot X_A \right) \cdot \mathrm{d}V\), ou encore \(\mathrm{d}V = \frac{Q_v}{k} \cdot \frac{\mathrm{d}X_A}{\left( 1 - X_A \right) \cdot \left( c + a \cdot X_A \right)}\)

On décompose cette fraction : \(\frac{1}{\left( 1 - X_A \right) \cdot \left( c + a \cdot X_A \right)} = \frac{\alpha}{1 - X_A} + \frac{\beta}{c + a \cdot X_A}\). Pour retrouver les valeurs de \(\alpha\) et \(\beta\), on remet tout sur le même dénominateur : \(\frac{\alpha \cdot c + \alpha \cdot a \cdot X_A + \beta - \beta \cdot X_A}{\left( 1 - X_A \right) \cdot \left( c + a \cdot X_A \right)}\). Il faut donc que \(\alpha \cdot a - \beta = 0\), donc \(\beta = \alpha \cdot a\) et que \(\alpha \cdot c + \beta = 1\), soit \(\alpha \cdot c + \alpha \cdot a = 1\) ; d'où \(\alpha =\frac{1}{a+c}\) et \(\beta =\frac{a}{a+c}\)

Donc \(\mathrm{d}V = \frac{Q_v}{k} \cdot \frac{1}{a+c} \cdot \left[ \frac{\mathrm{d}X_A}{1 - X_A} + a \cdot \frac{\mathrm{d}X_A}{c + a \cdot X_A} \right]\)

D'où \(V_{piston} = \frac{Q_v}{k} \cdot \frac{1}{a+c} \cdot \left[ \int\limits_{0}^{X_A^s}{\frac{\mathrm{d}X_A}{1 - X_A}} + a \cdot \int\limits_{0}^{X_A^s}{\frac{\mathrm{d}X_A}{c + a \cdot X_A}} \right] = \frac{Q_v}{k} \cdot \frac{1}{a+c} \cdot \left[ -\ln \ \left( 1 - X_A^s \right) + \frac{a}{a} \cdot \ln \ \frac{c + a \cdot X_A^s}{c} \right]\)

Finalement \(V_{piston} = \frac{Q_v}{k} \cdot \frac{1}{a+c} \cdot \ln \ \left( \frac{1 + \frac{a}{c} \cdot X_A^s}{1 - X_A^s} \right) =\)9,4 m³ (toujours pour \(X_A^s =\) 0,90)

RAC de 3,1 m³ jusqu'à la conversion de 48,3% puis TUB de 3,8 m³ jusqu'à la conversion de 90%

Traçons \(\frac{C_{A0}}{r} = \frac{a}{k \cdot a \cdot \left( 1- X_A \right) \cdot \left( c + a \cdot X_A \right)} = \frac{1}{k \cdot \left( 1- X_A \right) \cdot \left( c + a \cdot X_A \right)}\) vs \(X_A\) :

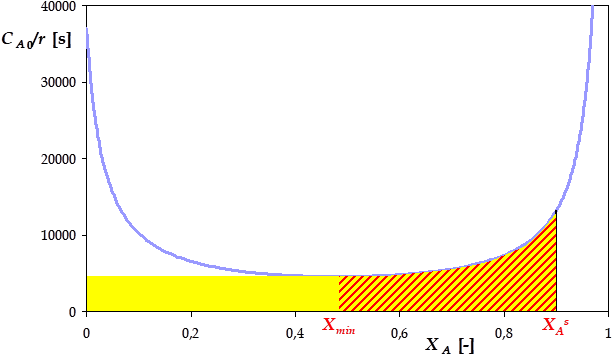
L'optimum consiste à associer un RPA puis en réacteur piston en série. Le RPA (aire colorée en jaune ci-dessus) doit conduire au taux de conversion \(X_A^{min}\), puis le réacteur piston (aire hachurée de rouge) jusqu'au taux de conversion souhaité \(X_A^s\).

Pour calculer \(X_A^{min}\), on dérive \(\frac{C_{A0}}{r}\) par rapport à \(X_A\) :

\(\frac{\mathrm{d}{C_{A0}}/{r}}{\mathrm{d}X_A} = - \frac{1}{k} \cdot \frac{\frac{\mathrm{d}\left( \left( 1 - X_A \right) \cdot \left( c + a \cdot X_A \right) \right)}{\mathrm{d}X_A}}{\left( 1 - X_A \right)^2 \cdot \left( c + a \cdot X_A \right)^2} = - \frac{1}{k} \cdot \frac{a \cdot \left( 1 - X_A \right) - \left( c + a \cdot X_A \right)}{\left( 1 - X_A \right)^2 \cdot \left( c + a \cdot X_A \right)^2} = - \frac{1}{k} \cdot \frac{a - c - 2 \cdot a \cdot X_A}{\left( 1 - X_A \right)^2 \cdot \left( c + a \cdot X_A \right)^2}\)

Cette dérivé s'annule lorsque le nominateur \(a - c - 2 \cdot a \cdot X_A\) est nul, soit pour \(X_A^{min} = \frac{a-c}{2 \cdot a} =\) 48,3%

On peut alors calculer le volume du premier réacteur à partir de l'expression établie précédemment pour le réacteur parfaitement agité, mais en allant seulement jusqu'à un taux de conversion \(X_A^{min}\) :\(V_{RAC} = \frac{Q_v}{k} \cdot \frac{a \cdot X_A^{min}}{a \cdot \left( 1 - X_A^{min} \right) \cdot \left( c + a \cdot X_A^{min} \right)} =\) 3,1 m³

Pour le second réacteur, il faut reprendre l'intégration entre \(X_A^{min}\) et \(X_A^s\) : \(V_{TUB} = \frac{Q_v}{k} \cdot \frac{1}{a+c} \cdot \left[ \ln \ \left( \frac{c + a \cdot X_A^s}{c + a \cdot X_A^{min}} \right) - \ln \ \left( \frac{1-X_A^s}{1-X_A^{min}} \right) \right] =\) 3,8 m³

Soit 6,9 m³ au total pour les deux réacteurs.

Le gain par rapport au volume du réacteur piston pur n'est pas énorme. Il n'est pas sûr qu'il soit dans ce cas pertinent de construire deux réacteurs, même s'ils ont un volume global inférieur... Une évaluation économique serait nécessaire pour avoir une réponse définitive sur cet optimisation.