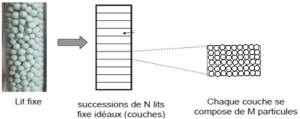
Stratégie de dimensionnement d'un réacteur catalytique à lit fixe : les étapes-clés
Détermination du réactif clé
Toute la démarche de dimensionnement va consister à comparer les vitesses de migration et de réaction au sein du réacteur pour un réactif clé. On raisonnera alors sur l'espèce ayant la mobilité diffusionnelle la plus faible. Pour tous les réactifs \(j\) en présence, on comparera le produit de leur concentration (moyenne) dans le réacteur et de leur diffusivité moléculaire dans le mélange, soit \(\frac{D_j \cdot C_j}{\nu_j}\) (\(\nu_j\) étant le coefficient stœchiométrique de l'espèce \(j\) (en valeur absolue) dans la réaction). Cela équivaut à comparer les modules de THIELE des réactifs.
On bâtira alors la démarche de dimensionnement pour l'espèce réactive admettant la valeur de \(\frac{D_j \cdot C_j}{\nu_j}\) la plus faible. Il s'agira souvent du réactif en concentration faible devant celles des autres réactifs, et/ou de la molécule de plus grande taille.
Choix de l'objet catalytique
Pour réaliser une réaction chimique en catalyse hétérogène à l'échelle industrielle, le choix de l'objet catalytique qui sera placé en lit fixe dans le réacteur est crucial. En effet, cet objet catalytique, idéalement, doit minimiser la résistance au transfert diffusionnel interne, donc être suffisamment petit pour permettre un module de THIELE si possible inférieur à 0,3 (régime chimique) ou au moins inférieur à 1 (début du régime intermédiaire), mais également suffisamment gros pour éviter que les pertes de charges ne soient rédhibitoires.
Il est communément admis que des grains de catalyseur dont la dimension est inférieure à 1 mm ne sont pas acceptables (du point de vue des pertes de charge engendrées).
Lorsqu'une dimension inférieure à 1 mm est nécessaire pour avoir un catalyseur suffisamment efficace, on peut envisager des particules imprégnées de matériau catalytique actif sur leur périphérie uniquement, particules dites "en coquille d'œuf".
La démarche est alors la suivante :
Pour le réactif clé (identifié à l'étape précédente), on calcule le coefficient de diffusion effective dans les grains, en tenant compte des caractéristiques (porosité, tortuosité des pores, diamètre des pores) de la matrice-support (alumine, oxyde de titane, céramique...).
On identifie l'expression du module de THIELE adapté à l'ordre de la réaction ou à son type de loi cinétique. En vue de son évaluation numérique, on calculera les concentrations des réactifs intervenant dans l'expression de \(\varphi_s\) à l'entrée du réacteur mais aussi à la sortie (balayant ainsi toute la gamme des concentrations). En vue de son évaluation numérique, on calculera les concentrations des réactifs intervenant dans l'expression de \(\varphi_s\) à l'entrée du réacteur mais aussi à la sortie (balayant ainsi toute la gamme des concentrations). Dans le cas où la réaction diffère d'un ordre 1, on néglige dans un premier temps les gradients externes de concentration en prenant \(C_s = C_e\). Ces derniers sont examinés par la suite.
On calcule la dimension caractéristique \(L\) des grains plaçant le réacteur en limite du régime chimique (à l'entrée comme à la sortie du réacteur), c'est-à-dire autorisant \(\varphi_s=0,3\) (cas idéal). On rappelle : \(L=\frac{d_p}{6}\) pour une sphère imprégnée de matériau catalytique actif jusqu'au cœur, \(L=e\) pour des grains en coquille d'œuf, \(L=\frac{d_p}{4}\) pour un cylindre imprégné jusqu'au cœur.
Si les particules doivent être en coquille d'œuf, il faut tenir compte des contraintes de leur fabrication : en général, les fabricants de catalyseur ne proposent que des épaisseurs de coquilles multiples de 100 µm (ou égales au minimum à 50 µm).
Ainsi, il n'est pas toujours possible d'assurer le régime chimique pour le réacteur. Il faut alors évaluer précisément \(\varphi_s\) et \(\eta_s\) avec la valeur de \(L\) choisie, et ce pour les conditions d'entrée comme pour les conditions de sortie du réacteur. On observera au passage si ces grandeurs varient peu ou beaucoup le long du réacteur.
Pré-dimensionnement du réacteur sous l'hypothèse d'isothermicité
Le type de particule catalytique étant choisi, on procède au pré-dimensionnement u réacteur, en se basant sur les hypothèses simplificatrices suivantes :
réacteur en régime permanent ;
écoulement idéal de type « piston » dans le réacteur ;
réacteur isotherme, c'est-à-dire suffisamment bien refroidi (ou réchauffé, selon la thermicité de la réaction) pour que les gradients de température au sein du réacteur soient négligeables.
A noter que les autres types de politiques thermiques, plus réalistes, que l'on pourra ensuite considérer pour le réacteur sont :
réacteur adiabatique (c'est-à-dire parfaitement calorifugé) ;
réacteur avec température de paroi constante (c'est-à-dire plongé dans une enceinte parcourue par un fluide caloporteur circulant à vitesse élevée).
Attention :
Dans tout ce qui suit, on se place dans le cas de figure où toute la particule est active (ou la phase catalytique est déposée de façon homogène jusqu'au cœur).
On écrit le bilan de conservation de l'espèce réactive clé A sur une « tranche » fine du réacteur à lit fixe :
\(\mathrm{d} F_A = - \overline{r} \cdot \mathrm{d} V_{cata}\)
ou : \(\frac{\mathrm{d} (v_z \cdot C)}{\mathrm{d} z} + \eta_s \cdot (1 - \varepsilon) \cdot r_s = 0\) (eq. BM)
\(V_{cata} = (1-\varepsilon) \cdot V\) (donc \(\overline{r} \cdot (1-\varepsilon) = \eta_s \cdot r_s \cdot (1-\varepsilon) = \eta_s \cdot \rho_B \cdot rm\))
avec \(\varepsilon\) : degré de vide du lit (=0,4 pour des sphères)
\(rm\) : vitesse de réaction massique intrinsèque (mol s-1 kgcata-1)
\(v_z\) : vitesse superficielle du gaz (m s-1)
\(\rho_B\) : masse volumique du lit (kg mlit-3)
On intègre ce bilan jusqu'à la concentration de sortie désirée pour le réactif A (c'est-à-dire jusqu'au taux de conversion voulu), et on identifie le volume de catalyseur nécessaire \(V_{cata}\) correspondant.
Ainsi, pour une réaction d'ordre 1 et réalisée en phase liquide (ou en phase gaz mais n'induisant pas de variation du nombre total de moles, donc pas de variation du débit volumique global), \(V_{cata}\) est calculé aisément par intégration analytique de l'équation (eq. BM) :
\(V_{cata} = - \frac{Q}{\eta_s \cdot k} \cdot ln (1-X_{sortie})\)
Attention :
En phase gaz, s'il y a variation du nombre de moles, de température ou de pression, il y a variation du débit volumique \(Q\), et donc de \(v_z\).
Minimisation des résistances par transferts externes et calcul de la perte de charge
Méthode :
Ayant obtenu un ordre de grandeur du volume du catalyseur contenu dans l'appareil, on peut en déduire le volume \(V\) de l'appareil. On procède alors au dimensionnement plus fin du réacteur isotherme.
On choisit d'abord une vitesse superficielle de circulation du fluide dans le réacteur, \(v_z\) , qui, pour le débit volumique \(Q\) à satisfaire, conditionne la valeur de la section droite de l'appareil, donc son diamètre \(D_t\).
Pour guider ce choix :
pour un gaz, \(v_z\) vérifie 0,1< \(v_z\) <10 m s-1
pour un liquide, \(v_z\) vérifie 0,001< \(v_z\) <0,1 m s-1
Ensuite on peut déterminer les dimensions du réacteur isotherme (supposé de forme cylindrique) en se basant sur la valeur du volume \(V\) : \(L_R\), \(D_t\), en respectant le rapport d'aspect 1< \(\frac{L_R}{D_t}\) <20, qui assure au réacteur une longueur grande devant son diamètre, rendant l'établissement d'un régime d'écoulement piston crédible.
On testera alors la valeur choisie pour la vitesse \(v_z\) en vérifiant successivement plusieurs critères.
Vérification d'une résistance externe de masse et de chaleur minime
On écrit la continuité du flux de masse du réactif clé à la surface du grain de catalyseur (de surface \(S\)) : \(k_D \cdot (C_e-C_s) \cdot S= \overline{r} \cdot V_P\), où \(k_D\) est le coefficient de transfert de masse convectif à proximité du grain.
Estimation des écarts \((C_e-C_s)\) : \(k_D \cdot (C_e-C_s)= \overline{r} \cdot L\) (calculé en entrée du réacteur)
De même, la conservation du flux de chaleur à la surface du grain permet d'écrire :
Estimation des écarts \((T_e-T_s)\) : \(h \cdot (T_e-T_s)= \overline{r} \cdot L\cdot \Delta_R H\) (calculé en entrée du réacteur)
Note : on rappelle qu'on note \(C_e\) et \(C_s\) la concentration d'un réactif-clé à l'extérieur du grain et en surface du grain (respectivement). De façon similaire, \(T_e\) et \(T_s\) sont les températures régnant à l'extérieur et en surface du grain (respectivement).
On doit vérifier que \((C_e-C_s)\) est faible devant \(C_e\). On doit aussi avoir \((T_e-T_s)\) faible (moins de quelques degrés).
Pour réduire ces gradients, on peut augmenter la vitesse du fluide (ou réduire la taille des particules) – voir les corrélations donnant \(Sh\) ou \(Nu\) – mais cela conduit à augmenter la perte de charge. Un compromis doit donc être trouvé sur la valeur de la vitesse de circulation du fluide, pour respecter \(\Delta P_{max}\).
Estimation de la perte de charge
On écrit le bilan de quantité de mouvement sur une ‘tranche' infinitésimale d'épaisseur \(\mathrm{d}z\) dans le réacteur :
\(- \frac{\mathrm{d}P}{\mathrm{d}z} = \frac{f \cdot \rho_G \cdot v_z^2}{d_p}\) avec \(f = \frac{1-\varepsilon}{\varepsilon^3} \cdot \left( 1,8 + 180 \cdot \frac{1-\varepsilon}{Re} \right)\) (loi d'Ergun)
où \(f\) est le facteur de friction
En général on tolère une perte de charge globale sur le réacteur de 30% de la valeur de la pression opératoire.
Si l'un ou plusieurs de ces 3 critères ne sont pas vérifiés, il faut remettre en question la valeur choisie pour \(v_z\). On pourra aussi dans certains cas, pour réussir à satisfaire tous les critères, remettre en question la taille \(d_p\) des particules (à laquelle \(\Delta P\) est également sensible).
Si les gradients de concentration ou de température ne peuvent être malgré tout négligés, il faut en tenir compte en recalculant le module de THIELE, avec \(C_s\) (et \(T_s\)) qui diffère(nt) donc de \(C_e\) (et \(T_e\)), puis l'efficacité du catalyseur, qu'on pourra évaluer en tenant compte de la résistance par transfert externe avec :
\(\frac{1}{\eta_e} = \frac{1}{\eta_e} + \frac{\varphi_s^2}{Bi_m}\)
Contrôle de la température interne et choix des tubes
On prend ici en compte la chaleur produite par la réaction (ou consommée, dans le cas d'une réaction endothermique), et, pour contrôler au mieux la température régnant dans le réacteur (et donc sa productivité et sa sélectivité), on envisage une configuration multi-tubulaire pour ce réacteur, qui devient donc un « réacteur-échangeur ».
On doit identifier le diamètre des tubes \(d_t\) qui offrira une aire d'échange suffisante pour l'échange thermique à satisfaire, et \(n_t\), le nombre de tubes nécessaires pour accueillir le débit voulu. La longueur des tubes est \(L_R\) (longueur du réacteur) ; la valeur de \(L_R\) qui était utilisée lors des calculs isotherme peut être un peu modifiée ici puisqu'on prend en compte maintenant les phénomènes thermiques, impliquant que la température du fluide dans le réacteur n'est plus strictement uniforme.
On écrit le bilan thermique sur le fluide qui s'écoule dans le réacteur (à l'intérieur des tubes), pour une "tranche" de largeur infinitésimale \(\mathrm{d}z\) présente dans le réacteur :
On considère que le réacteur a une température de paroi \(T_p\) constante (on prend en général \(T_p=T_e\)).
\(\mathrm{d} \phi = F_{A0} \cdot \mathrm{d}X \cdot \Delta_R H(T) + F_0 \cdot \Gamma_p \cdot \mathrm{d}T\), avec \(F_0 \cdot \Gamma_p =\sum F_j \cdot Cp_j =Q \cdot \rho_F \cdot cp_m\)
Le flux de chaleur convectif en paroi vaut \(\mathrm{d} \phi = h_w \cdot a \cdot (T_p-T) \cdot \mathrm{d}V\)
ou encore : \(\frac{4}{d_t} \cdot h_w \cdot (T_p-T) = (1-\varepsilon_{lit}) \cdot \eta_s \cdot r_s \cdot \Delta H + v_z \cdot \rho_F \cdot cp_m \cdot \frac{\mathrm{d}T}{\mathrm{d}z}\) (eq. BTh)
avec \(a\) : surface spécifique du réacteur (m2 m-3) ; \(a = \frac{4}{d_t}\) pour un tube de diamètre \(d_t\)
\(cp_m\) : capacité calorifique moyenne du fluide (J kg-1 K-1)
\(h_w\) : coefficient de transfert thermique en paroi (W m-2 K-1)
avec \(r(C,T)\), \(v_z\), \rho_F et \(cp_m\) variables le long de \(z\)
Attention :
Si les particules catalytiques sont en coquille d'œuf, il faut pondérer la vitesse de réaction, non seulement par \((1-\varepsilon_{lit})\), mais aussi par la quantité de catalyseur contenue dans les particules, soit \(\varepsilon_{coquille}\).
On détermine le diamètre des tubes \(d_t\) par vérification du caractère isotherme approché : on considère la cote axiale \(z\) du réacteur où la température maximale \(T_{max}\) (ou minimale \(T_{min}\), dans le cas d'une réaction endothermique) est atteinte. À cette cote le terme dérivé, dans le bilan thermique, est localement nul, et il reste :
\(d_t = \frac{4 \cdot h_w \cdot (T_{max}-T_p)}{(1-\varepsilon_{lit}) \cdot \eta_s \cdot r_s \cdot (- \Delta_R H)}\)
Dans cette expression :
\(r_s\) et \(\eta_s\) sont calculés à \(T_{max}\) (\(T_{max}\) donnée ou à fixer), et \(r_s\) doit éventuellement être pondérée par \(\varepsilon_{coquille}\) (voir plus haut).
la valeur limite de température, \(T_{max}\), peut être liée à différents facteurs, comme la température de dégradation du catalyseur, la vaporisation des réactifs dans le cas d'une réaction en phase liquide, au risque d'emballement thermique pour une réaction exothermique (risque dû à la variation exponentielle de la vitesse de réaction avec la température, intimement liée à l'énergie d'activation de la réaction considérée), ou la température à partir de laquelle la vitesse d'une réaction secondaire n'est plus négligeable. Dans ce dernier cas, si on dispose des lois cinétiques des réactions secondaires, cette température limite peut être évaluée facilement.
\(T_p\) est souvent prise égale à \(T_e\) en première approche,
\(h_w\) est calculé, par exemple, par la corrélation de Léva, valable pour un gaz semblable à l'air : \(\frac{h_w \cdot d_t}{\lambda_G} = 2 \cdot Re^{0,8} \cdot exp \left( -6 \cdot \frac{d_p}{d_t}\right)\) pour 20 < \(Re_p\) < 7600 et 0,05 < \(\frac{d_p}{d_t}\) < 0,3.
Dans le cas d'un liquide, on peut utiliser la corrélation de Yagi et Wakao (1959) :
\(Nu_{w,L} = \frac{h_w \cdot d_t}{\lambda_L} = 0,6 \cdot Pr_L^{1/3} \cdot Re_L^{0,5}\) pour 1 < \(Re_L\) < 40
\(Nu_{w,L} = \frac{h_w \cdot d_t}{\lambda_L} = 0,2 \cdot Pr_L^{1/3} \cdot Re_L^{0,8}\) pour 40 < \(Re_L\) < 2000
Vu que \(d_t\) est exprimé en fonction de \(h_w\), qui est lui-même fonction de \(d_t\), on procédera par tâtonnement, en testant des valeurs pertinentes de \(d_t\) pour l'industrie (1 pouce ; 0,5 pouce ; etc.). L'utilisation d'un solveur ne donnera pas de solution réaliste.
Dimensionnement précis : couplage des bilans de masse, de chaleur, d'énergie
Dans cette étape ultime, on procède à l'intégration couplée des bilans différentiels de masse et de chaleur (équations BM et BTh, voir plus haut), afin de calculer pas à pas, le long des tubes du réacteur, l'évolution du taux de conversion de la réaction et l'évolution de la température.
On procédera à l'aide d'un outil numérique : tableur, ou script d'appel à des méthodes de résolution d'équations différentielles ordinaires couplées (méthode "ode45", par exemple).
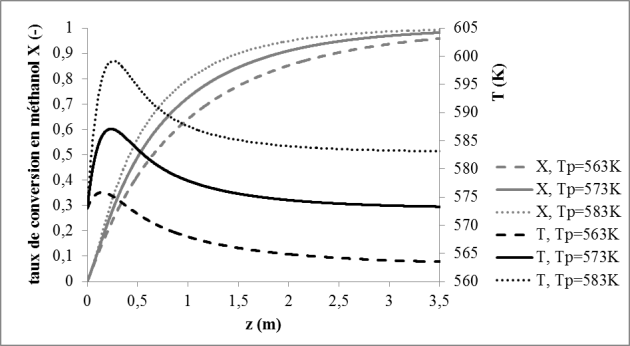
On peut alors tracer \(X\) et \(T\) le long de la cote axiale du réacteur, et observer leur comportement. Ces tracés sont des outils cruciaux, permettant de poser un diagnostic, et de modifier des paramètres pour améliorer le fonctionnement du réacteur ; par exemple :
Si le taux de conversion stagne en fin de réacteur, on peut décider de raccourcir l'appareil.
Si la température augmente trop violemment dans le réacteur, on peut diminuer le diamètre des tubes, et/ou diminuer la température de paroi, et/ou diminuer la température d'alimentation, et/ou remettre en question les choix faits sur la vitesse de circulation du fluide ou même sur la configuration des particules de catalyseur.