Exemple de dimensionnement d'un réacteur catalytique à lit fixe : réacteur de production de formaldéhyde
La réaction d'oxydation du méthanol en formaldéhyde sur catalyseur Fe-Mo est du premier ordre :
\(r_s = k_s \cdot C_m\) avec \(k_s\) = 5 10-4 cm s-1 à 300°C
Données :
\(\Delta H_R\) = - 38 500 cal mol-1 (de formol formé)
Ea =19 000 cal mol-1
Catalyseur :
\(\rho_p\) = 1,1 g cm-3 ; \(\varepsilon_p\) = 0,66 ; \(\tau_p\) =4 ; \(d_p\) = 50 \({\buildrel _{\circ} \over {\mathrm{A}}}\)
\(S_i\) =105 cm2 g-1 ; \(\lambda_{ef}\) = 5 10-4 cal cm-1 s-1 K-1
Gaz :
\(D_m\) = 5 10-5 m2 s-1 ; \(C_p\) = 0,25 cal g-1 K-1 ; \(\rho_G\) = 0,62 kg m-3
\(\mu_G\) = 0,25 10-4 Pa s ; \(\lambda\) =1,1 10-4 cal cm-1 s-1 K-1
Question
Concevoir un réacteur à lit fixe d'oxydation du méthanol en formaldéhyde sur catalyseur Fe-Mo.
Conditions d'entrée : 300°C ; pression atmosphérique ; fraction molaire de méthanol 3% dans l'air.
Production visée : 1 t/h de formaldéhyde, avec un taux de conversion de 99%
On supposera tout d'abord le réacteur isotherme, puis on envisagera l'aspect thermique (réacteur à température de paroi constante).
Contrainte : température maximale 350°C.
Solution détaillée
Dans ce travail, les calculs de pré-dimensionnement sont effectués en considérant d'abord le réacteur isotherme (pour simplifier les calculs). Dans un 2e temps (paragraphes 6 et 7), on verra comment rendre l'appareil aussi proche que possible de l'hypothèse isotherme.
Réaction et cinétique
CH3OH + ½ O2 \(\rightarrow\) CH2O + H2O
Conversion en unité S.I. de la constante cinétique à 300°C :
\(k_s\) = 5 10-4 cm s-1 ; \(k_i = k_s \cdot S_i \cdot \rho_{particule}\), ainsi \(k_i\) = 55 s-1
Remarque : dans le domaine de la catalyse hétérogène, une constante de vitesse exprimée en s-1 (ou min-1) donne généralement une vitesse de réaction en mol m3cata s-1 (si les scientifiques qui ont identifié la cinétique l'ont bien exprimée par unité de volume de catalyseur et non de réacteur).
Identification du réactif limitant
A ce stade, on doit, en toute rigueur, identifier l'espèce réactive dont la migration diffusionnelle dans le grain de catalyseur sera limitante, c'est-à-dire (si on se réfère au dénominateur du module de Thiele et en considérant que les coefficient \(D_{m,i}\) et \(D_{e,i}\) varient dans les mêmes proportions pour les différentes espèces) celle dont le terme \(\frac{D_{m,i} \cdot C_i}{\nu_i}\) sera le plus faible.
Dans l'exemple traité, il faudrait donc connaître les coefficients de diffusion moléculaires dans l'air du méthanol et de l'oxygène.
Mais ici, le méthanol est présent en faible concentration dans le courant gazeux alimentant le réacteur ; de plus, la taille de la molécule de méthanol est grande devant celle de l'oxygène, et il est consommé deux fois plus vite que l'oxygène par la réaction considérée. On admet donc implicitement que le méthanol est l'espèce qui diffuse le moins rapidement dans le matériau catalytique, et qu'il sera donc l'espèce limitante pour la réaction, dans le grain. C'est au méthanol que la donnée \(D_m\) de l'énoncé se réfère, et c'est pour le méthanol qu'on calculera \(D_P\), \(D_K\), \(D_e\), \(\Phi_s\), \(\eta_s\)...
Calcul de la taille des grains de catalyseur
Dans un premier temps on suppose négligeables les gradients de concentration et de température dans la couche limite autour des grains de catalyseur (résistance externe aux transferts négligeable), donc \(C_s = C_e\) et \(T_s = T_e\).
Coefficient de diffusion dans les grains :
\(\frac{1}{\mathcal{D}} = \frac{1}{D_K} + \frac{1}{D} \) avec \(D_K = \frac{1}{3} \cdot \delta_p \cdot \sqrt{\frac{8 \cdot \mathbb{R} \cdot T}{\pi \cdot M}}\)
\(D_K =\) 1,026 10-6 m2 s-1
D'où \(\mathcal{D} =\)1,005 10-6 m2 s-1 et \(D_e = \frac{\varepsilon_p \cdot \mathcal{D}}{\tau_p} =\) 1,66 10-7 m2 s-1
Calcul du module de Thiele \(\varphi_s\) :
\(\varphi_s = \frac{d_p}{6} \cdot \sqrt{\frac{k_i}{D_e}} =\) 0,3 (régime chimique) d'où \(d_p =\) 9,88 10-5 m, soit environ 100 µm
Cette taille de particule est trop faible : les pertes de charges dans un réacteur rempli de ces grains seraient trop élevées.
On choisit un catalyseur de type "coquille d'œuf", de diamètre 1 mm (valeur de départ), et comprenant une couche de catalyseur d'épaisseur \(e\) telle que \(\varphi_s = e \cdot \sqrt{\frac{k_i}{D_e}}\) = 0,3.
Finalement on prendra \(e\) = 50 µm
Calcul de \(\varphi_s\) et \(\eta_s\) exacts pour ces grains de catalyseur :
\(\varphi_s = e \cdot \sqrt{\frac{k_i}{D_e}} =\) 0,910 et \(\eta_s = \frac{\mathrm{th \:} \varphi_s}{\varphi_s}\) = 0,792.
Le réacteur fonctionne en régime intermédiaire.
Le réacteur étant d'abord considéré isotherme, les valeurs de \(\varphi_s\) et \(\eta_s\) sont constantes dans tout l'appareil.
Dimensionnement du réacteur isotherme
Conservation du débit total de gaz
Pour 100 moles de gaz présentes dans le courant d'alimentation du réacteur, en sortie de réacteur 3 x 0,99 moles de méthanol et 1,5 x 0,99 moles de O2 ont disparu, et 6 x 0,99 moles d'autres gaz sont apparues. On retrouve au total 101,5 moles de gaz environ.
Le débit molaire total de gaz, et donc (en conditions isothermes et isobares) le débit volumique total de gaz, \(Q\), varient donc de 1,5% seulement à la traversée du réacteur. La dilatation volumique est négligeable dans ce réacteur.
En tenant compte des proportions molaires du méthanol et de l'oxygène dans le courant gazeux qui alimente le réacteur, et la température et de la pression souhaitées dans l'appareil, on calcule au passage que ce débit volumique total de gaz, à l'entrée du réacteur, vaut 17,50 m3 s-1.
Volume du réacteur isotherme
On peut alors appliquer la relation (valable pour une réaction d'ordre 1) :
\(V_{cata} = \frac{-Q}{\eta_s \cdot k_i} \cdot ln (1 - X_{As})\). On trouve \(V_{cata} =\) 1,85 m3.
Ce volume représente le volume de catalyseur nécessaire pour réaliser 99% de conversion. Ce volume est uniquement constitué des couronnes de support qui ont été imprégnées de substances actives sur chaque particule ("coquilles"). On calcule alors le volume occupé par les billes, puis le volume du cylindre qui contient le lit de billes :
\(V_{cata \: dans \: particule} = \frac{4}{3} \pi \cdot R^3 - \frac{4}{3} \pi \cdot (R - e)^3\)
\(\frac{V_{cata \: dans \: particule}}{V_{particule}} = \frac{R^3 - (R - e)^3}{R^3} \approx \frac{3 e}{R}\), qu'on notera \(\varepsilon_{coquille}\).
Ainsi : \(V_{cata} = V_{reacteur} \cdot (1- \varepsilon_{lit}) \cdot \varepsilon_{coquille}\), et donc :
\(V_{reacteur} = \frac{V_{cata}}{(1- \varepsilon_{lit}) \cdot \varepsilon_{coquille}} \approx V_{cata} \cdot \frac{R}{3 e} \cdot \frac{1}{1-\varepsilon_{lit}} =\) 10,27 m3.
Pour ce réacteur on pourrait prendre par exemple un cylindre de longueur 6 m et de diamètre 1,48 m.
Analyse des transferts externes
Choix d'une vitesse (superficielle) de circulation des gaz
On choisit une vitesse \(v_z\) dans la gamme [0,1 ; 10] m/s, par exemple \(v_z \approx\) 5 m/s.
Pour cette vitesse la section droite du réacteur est \(S = \frac{Q}{v_z}\) soit 3,5 m2. Les dimensions du réacteur, respectant \(V_{reacteur} =\) 10,27 m3, seraient donc \(D_t =\) 2,11 m et \(L_R =\) 2,94 m (ce qui respecte 1 < \(L_R/D_t\) < 20).
Estimation du gradient de masse près du grain (face externe)
Calcul de \(k_D\) : \(Sh = \frac{k_D \cdot d_p}{D} = 2,0 + 1,8 \cdot Re^{1/2} \cdot Sc^{1/3}\)
On estime \(Re = \frac{\rho \cdot u \cdot d_p}{\mu} \approx \frac{0,62 \times 5 \times 1 \cdot 10^{-3}}{0,25 \cdot 10^{-4}} = \) 124
On estime \(Sc = \frac{\mu}{\rho \cdot D} \approx \frac{0,25 \cdot 10^{-4}}{0,62 \times 5 \cdot 10^{-5}} =\) 0,8
Alors \(S_h =\) 20,67 et \(k_D =\) 0,94 m/s.
Le gradient massique externe est alors donné par : \(C_e - C_s = \frac{r_{app} \cdot L}{k_D}\), en prenant ici \(C_s \approx C_A^e = 0,03 \times \frac{101325}{8,32 \times 573} =\) 0,637 mol/L
On trouve \(\frac{C_e - C_s}{C_s} =\) 0,23%. Ce gradient est négligeable.
Estimation du gradient thermique près du grain
Calcul de h : \(Nu = \frac{h \cdot d_p}{\lambda} = 2,0 + 1,8 \cdot Re^{1/2} \cdot Pr^{1/3}\)
On a toujours \(Re =\)124.
On estime \(Pr = \frac{C_p \cdot \mu}{\lambda} \approx \frac{0,25 \times 4,18 \times 1000 \times 0,25 \cdot 10^{-4}}{1,1 \cdot 10^{-2} \times 4,18} =\) 0,568
Alors \(Nu =\) 18,63 et \(h =\) 204,96 W m-1 K-1.
Le gradient thermique externe est alors donné par : \(T_e - T_s = \frac{r_{app} \cdot L \cdot \Delta_R H}{h} = \frac{\eta_s \cdot k_i \cdot C_s \cdot \Delta_R H}{h}\), avec \(T_e =\) 573 K, avec \(L = e\).
On trouve \(T_s =\) 574,1 K, ce qui est très proche de \(T_e\) (1,1 K d'écart : insignifiant devant \(T_e =\) 573 K).
Pour \(d_p =\) 1 mm et \(v_z =\) 5 m/s, les transferts externes ne sont pas limitants pour la réaction chimique.
Évaluation des pertes de charge
On trouve \(f =\) 25,04 et \(- \frac{\Delta P}{\Delta z} =\) 388 125 Pa/m. Cela donne \(\frac{\Delta P}{P} =\) 11,24, donc la perte de charge est 11 fois plus élevée que la pression opératoire, ce qui est irréaliste.
On refait les calculs en diminuant \(v_z\). Ainsi \(v_z =\) 1,15 m/s permet d'obtenir cette fois \(\frac{\Delta P}{P} =\) 29%, ce qui est acceptable, tout en maintenant des gradients externes de concentration et de température négligeables. Cependant, cette vitesse implique \(D_t =\) 4,4 m et \(L_R =\) 0,68 m : le réacteur est beaucoup trop court devant son diamètre, le critère 1< \(L_R/D_t\) n'est plus vérifié.
Pour lever ce blocage, il faut remettre en question le diamètre des particules \(d_p\) (sans modifier la valeur de \(e\)), pris initialement à 1 mm par défaut. La perte de charge étant, en lit fixe, inversement proportionnelle à \(d_p\), il faut augmenter \(d_p\). On reprend tous les calculs et on converge pour \(d_p = \) 5 mm. Le tableau ci-dessous récapitule les différents résultats.
\(d_p\) mm | \(e\) µm | \(V_{cata}\) m3 | \(V_{reacteur}\) m3 | \(v_z\) m/s | \(L_R\) m | \(D_t\) m | \(Re\) - | \(Sh\) - | \(Nu\) - | \(k_D\) m/s | \(h\) W m-2 K-1 | \(\frac{C_e-C_s}{C_s}\) % | \(T_s\) K | \(\frac{\Delta P}{P}\) % |
5 | 50 | 1,85 | 51,4 | 1,5 | 4,40 | 3,85 | 186 | 24,9 | 22, 4 | 0,24 | 49,2 | 0,9 | 577 | 27 |
Choix des dimensions du réacteur
Vu la thermicité de la réaction, le réacteur doit être constitué de plusieurs tubes fins pour faciliter son refroidissement. On comprend ici que, dans ces conditions, le rapport d'aspect du réacteur vérifiera aisément \(L_R/D_t\) > 1.
Si la température varie le long des tubes, le bilan thermique différentiel s'écrit, au point de température maximale où \(\frac{\mathrm{d}T}{\mathrm{d}t} \) est nul : \(d_t = \frac{4 \cdot h_w \cdot (T_{max} - T_p)}{(1 - \varepsilon_{lit}) \cdot \varepsilon_{coquille} \cdot \eta_s \cdot r_s \cdot (-\Delta_R H)}\)
On prendra un diamètre de tube \(d_t\) standard, par exemple de 1 pouce (2,54 cm).
On prendra en première hypothèse \(T_p = T_e\). On limitera ici \(T_{max}\) arbitrairement (en l'absence d'autre information) à 350°C (623 K), comme le dit l'énoncé.
Si on a 0,05 < \(d_p/d_t\) <0,3, et également \(Re\) > 20, alors on peut estimer \(h_w\) par la corrélation de Leva : \(\frac{h_w \cdot d_t}{\lambda_G} = 2 \cdot Re^{0,8} \cdot exp \left( -6 \cdot \frac{d_p}{d_t}\right)\)
Pour \(v_z =\) 1,5 m/s, on a \(Re =\) 186, et pour \(d_t =\) 3 pouces, on trouve alors \(h_w\) = 53,2 W m-2 K-1, ce qui donne \(T_{max} =\) 630,6K. Cette température est correcte vis-à-vis de la limite fixée (633 K).
Remarquons que des tubes plus fins, par exemple \(d_t =\) 1 pouce, donneraient \(h_w\) = 72,7 W m-2 K-1, et \(T_{max} =\) 587,07K. Cette température est proche de \(T_e\) (573 K), conférant au réacteur un caractère quasi-isotherme.
Dans ce dernier cas, le nombre de tubes constituant le réacteur, calculé sur la base de la section droite totale du réacteur et de la section droite d'un tube unitaire, est de 23 027.
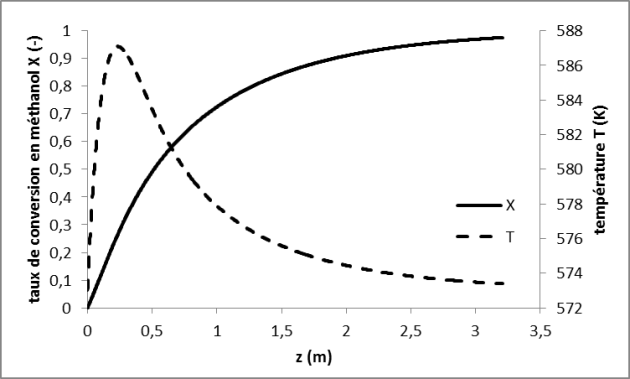
Caractérisation des variations de température dans l'appareil
Cette étude consiste à calculer pas à pas l'évolution couplée du taux de conversion et de la température à l'intérieur des tubes. Cette démarche peut être appliquée dans le cas d'un fonctionnement adiabatique ou pour le réacteur refroidi par la paroi.
On doit faire attention ici au fait que le module de Thiele \(\varphi_s\), et donc le facteur d'efficacité \(\eta_s\) et la vitesse apparente de réaction, varient le long de l'appareil puisque la température varie.
On observe qu'on retrouve, pour la valeur maximale de la température dans les tubes refroidis (ici \(T_{max} =\) 587,08 K à \(z =\) 0,23 m), une valeur très proche de la valeur de \(T_{max}\) évaluée au paragraphe précédent selon une démarche simplifiée (587,07 K). À noter que ce n'est pas toujours le cas, la vitesse de réaction étant généralement plus faible au point où la température vaut \(T_{max}\) que la valeur correspondant à l'entrée du réacteur (- valeur utilisée pour l'estimation de \(T_{max}\) - ; mais ici, l'augmentation de température en début de réacteur fait augmenter fortement la constante cinétique \(k\) (énergie d'activation élevée) : celle-ci vaut 82 s-1 au point de maximum de température, alors qu'elle valait 55 s\(-1\) à l'entrée du réacteur.
Enfin, à l'issue de l'intégration de \(T\) et \(X\) le long du réacteur, on peut recalculer le volume de l'appareil, qui doit être logiquement un peu plus faible que la valeur calculée sous l'hypothèse d'appareil isotherme puisque la température moyenne dans le réacteur refroidi est légèrement plus élevée que la température uniforme considérée dans le raisonnement isotherme. On obtient ici \(V_{reacteur} =\) 41,3 m3 (au lieu de 51,4 m3 par le calcul sous hypothèse de réacteur isotherme). Ce volume de réacteur (plus réaliste que le précédent) correspond donc à une longueur d'appareil plus faible \(L_R =\) 3,5m (au lieu de 4,4 m).