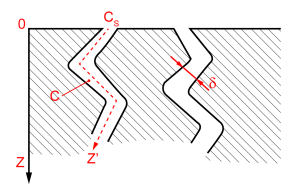
Transfert interne dans un grain poreux
Rappel :
Le vecteur densité de flux de matière s'écrit : \(\overrightarrow{N} = -D_e \cdot \overrightarrow{grad} \; C\), où \(D_e\)[1] = \(\frac{\varepsilon_p \cdot \mathcal{D}}{\tau_p}\) est la diffusivité effective, qui tient compte de la porosité interne des grains \(\varepsilon_p\)[2] et de la tortuosité des pores \(\tau_p\)[3] (notions rappelées ici).
Le vecteur densité de flux de chaleur s'écrit : \(\overrightarrow{\varphi} = -\lambda_e \cdot \overrightarrow{grad} \; T\), où \(\lambda_e\) est la conductivité thermique effective.
La relation concernant le transfert de matière est illustrée sur la figure ci-contre.
\(C_s\) est la concentration en surface de la particule et \(C\) la concentration dans les pores. Cette dernière varie en fonction de la distance par rapport à la surface du grain : \(C(z)\), selon la loi écrite précédemment.
Méthode : Diffusivité dans un gaz
Pour un gaz, la diffusivité \(\mathcal{D}\)[6] dans les pores est telle que : \(\frac{1}{\mathcal{D}} = \frac{1}{D_K} + \frac{1}{D} \), où \(D\)[7] est la diffusivité moléculaire et où la diffusivité de KNUDSEN[8] est donnée approximativement pour un gaz par \(D_K = \frac{1}{3} \cdot \delta_p \cdot \sqrt{\frac{8 \cdot \mathbb{R} \cdot T}{\pi \cdot M}} \approx 1,534 \cdot \delta_p \cdot \sqrt{\frac{T}{M}}\), \(\delta_p\)[9] étant le diamètre moyen des pores (cette relation est valable si ces pores ont une taille supérieure à environ 5 10-9 m), \(\mathbb{R}\)[10] la constante des gaz parfaits, \(T\)[11] la température de travail et \(M\)[12] la masse molaire.
Méthode : Diffusivité dans un liquide
Pour un liquide, la diffusivité \(\mathcal{D}\) dans les pores est égale à la diffusivité moléculaire \(D_j\) de l'espèce \(j\). Mais cette dernière dépend des flux des différentes espèces et des diffusivités moléculaires des binaires constitués par \(j\) avec chacune des autres espèces présentes ; elle est donc difficile à estimer.