Transport externe autour d'un grain
Considérons une particule poreuse au sein d'un fluide. Cette particule est entourée d'un film fluide au sein duquel se produit le transport externe et dans lequel il y a donc un profil de concentration[1] et un profil de température[2] : \(C_e\) est la concentration loin de la particule et \(C_s\) la concentration en surface de la particule ; \(T_e\) est la température loin de la particule et \(T_s\) la température en surface de la particule.
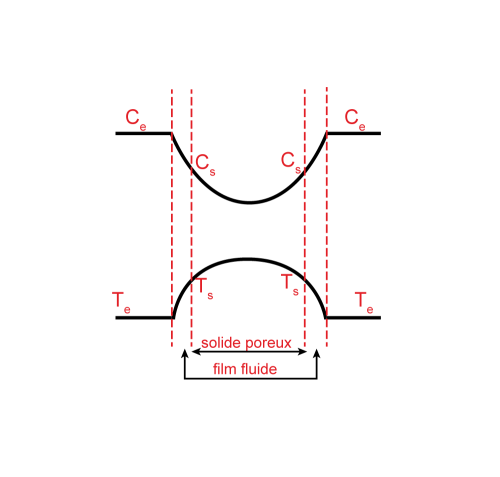
Il existe également un profil de concentration et un profil de température au sein de la particule, lié à la diffusion et à la conduction internes dans le grain poreux.
Rappel : Densités des flux
La densité de flux de matière[4] s'écrit \(N=k_D \cdot (C_e-C_s)\), où \(k_D\)[5] est la conductance de transfert de matière[5].
La densité de flux de chaleur[6] s'écrit \(\varphi=h \cdot (T_e-T_s)\), où \(h\)[7] est la conductance (ou coefficient) de transfert thermique[7].
Le transport externe se fait essentiellement par convection[8], d'où la forme des relations rappelées ci-dessus.
Méthode : Corrélation pour un lit fixe de particules
Dans le cas d'un lit fixe de particules, les corrélations de RANZ-LEVENSPIEL permettent d'estimer les conductances de transfert externe :
pour le transport de matière, le nombre de SHERWOOD[9] : \(Sh = \frac{k_D \cdot d_p}{D} = 2,0 + 1,8 \cdot Re^{1/2} \cdot Sc^{1/3}\)
pour le transport de chaleur, le nombre de NUSSELT[10] : \(Nu = \frac{h \cdot d_p}{\lambda} = 2,0 + 1,8 \cdot Re^{1/2} \cdot Pr^{1/3}\)
où on retrouve le nombre de REYNOLDS[11] \(Re = \frac{\rho \cdot u \cdot d_p}{\mu}\), le nombre de SCHMIDT[12] \(Sc = \frac{\mu}{\rho \cdot D}\) et le nombre de PRANDLT[13] \(Pr = \frac{\mu \cdot c_p}{\lambda}\),
avec \(u\)[14] la vitesse en fût vide, \(d_p\)[15] le diamètre équivalent des particules, \(\rho\), \(\mu\), \(D\), \(\lambda\) et \(c_p\) respectivement la masse volumique[16], la viscosité[17], la diffusivité moléculaire[18], la conductivité thermique[19] et la capacité calorifique massique[20] du fluide.
Méthode : Corrélation en milieu suspendu
Dans le cas d'un milieu suspendu (lit fluidisé ou transporté ; suspension agitée), le nombre de SHERWOOD[9] peut être estimé selon la corrélation :
\(Sh = 2 + \frac{1}{3} \cdot (Ar \cdot Sc)^{1/3}\)
avec le nombre d’ARCHIMÈDE défini par \(Ar = \frac{g \cdot d_p^3 \cdot \rho \cdot (\rho - \rho_s)}{\mu^2}\).
Remarque : Corrélation pour un grain seul
On trouve des corrélations de la forme \(Sh = 2,0 + 0,6 \cdot Re^{1/2} \cdot Sc^{1/3}\) et \(Nu = 2,0 + 0,6 \cdot Re^{1/2} \cdot Pr^{1/3}\) qui correspondent au cas d'un grain isolé.
Il existe évidemment de nombreuses autres corrélations pour estimer les coefficients de transfert, notamment pour des grains non sphériques ou bien si le fluide est soit un gaz soit un liquide.
Notion fondamentale : Ordres de grandeur
Pour les gaz, le nombre de SCHMIDT[12] et le nombre de PRANDLT[13] sont de l'ordre de 1.
Dans un liquide, le nombre de SCHMIDT[12] est de l'ordre de 1000.