Pertes de charge dans les accessoires
On entend par accessoire :
les vannes et robinets (le coefficient de singularité dépend alors non seulement du type de vanne et de sa technologie, mais aussi de l'ouverture de la vanne) ;
les organes de sécurité et de mesure (clapets, soupapes, débitmètres, ...) ;
les obstacles (grilles, chicanes, filtres, garnissages, ...).
Le mieux est alors de se reporter aux données du fournisseur de l'accessoire. On pourra également utiliser le "Mémento des pertes de charge" IDEL'CIK.
On donne ici quelques exemples, avant tout pour présenter les principaux types d'accessoires que l'on est susceptible de trouver sur une conduite.
Vannes à translation
Exemple : Vannes guillotine
La plus simple des vannes à translation est la vanne guillotine.

L'abaque ci-dessous permet de déterminer -en ordonnée- le coefficient de perte de charge singulière pour une vanne guillotine en fonction -en abscisse- de son degré d'ouverture. Celui-ci est exprimé comme le rapport entre la hauteur \(h\) au maximum de l'espace laissé libre pour l'écoulement du fluide (voir schéma à gauche) et le diamètre \(D\) de l'opercule.
Exemple : Vannes à membrane
Lorsque le liquide transporté est chargé ou corrosif, on pourra préférer utiliser une vanne à membrane (également appelée vanne à pincement).

Le coefficient de perte de charge d'une vanne à membrane est :
\(k=\left\{ \begin{array}{r l}& 2,3 - \rm{compl\grave{e}tement\ ouverte} \\& 2,6 - \rm{ouverte\ aux\ 3/4} \\& 4,3 - \rm{1/2\ ouverte} \\& 21 - \rm{1/4\ ouverte} \\\end{array} \right.\)
Exemple : Vannes à soupape et à pointeau
Pour terminer avec les vannes à translation voici la vanne à soupape et la vanne à pointeau, dont le principe est similaire. La partie conique de la vanne étant simplement plus effilée dans le cas d'un pointeau que pour une soupape.


On trouve dans la littérature, les ordres de grandeur suivants pour le coefficient de perte de charge :
vanne à soupape : \(k=\left\{ \begin{array}{r l}& 6,4 \quad - \quad \rm{compl\grave{e}tement\ ouverte} \\& 9,5 \quad - \quad \rm{\grave{a} demi ouverte} \\\end{array} \right.\)
vanne à pointeau : \(k=\left\{ \begin{array}{r l}& 9 \quad - \quad \rm{compl\grave{e}tement\ ouverte} \\& 13 \quad - \quad \rm{ouverte\ aux\ 3/4} \\& 36 \quad - \quad \rm{1/2\ ouverte} \\& 112 \quad - \quad \rm{1/4\ ouverte} \\\end{array} \right.\)
Remarque : Vannes de régulation
Pour les vannes de régulation, \(k\) est fonction (souvent exponentielle) du débit.
Vannes à rotation
Exemple : Vanne à boisseau sphérique
La vanne à boisseau sphérique est une vanne quart de tour. Elle est utilisée pour autoriser ou non la circulation du fluide dans une portion de conduite (vanne tout ou rien).

Les vannes à boisseau sphérique peuvent poser des problèmes de blocage lorsque le fluide transporté est chargé.
Exemple : Vanne papillon
La vanne papillon est elle-aussi une vanne quart de tour (tout ou rien).
L'inconvénient majeur des vannes papillon est qu'elles sont tendance à devenir "fuillardes". En effet lorsque la vanne est fermée, l'étanchéité est assurée uniquement par le contact entre le volet et la conduite le long du périmètre de ce volet, alors que dans le cas d'une vanne à boisseau sphérique l'étanchéité est assurée par une surface de contact bien plus grande entre le corps de vanne et la sphère.
L'autre inconvénient de ces vannes est que même ouverte complètement elles occasionnent une perte de charge non nulle due au contournement du volet. Au contraire, pour une vanne à boisseau sphérique complètement ouverte, l'écoulement du fluide n'est pratiquement pas perturbée.
Le coefficient de perte de charge pour la vanne papillon peut être calculé comme suit :
\(k=\frac{3,2\ {{10}^{7}}}{{{\left( 90-\alpha [{}^\circ ] \right)}^{4}}}\)
On trouve également des abaques telles que celles ci-dessous.
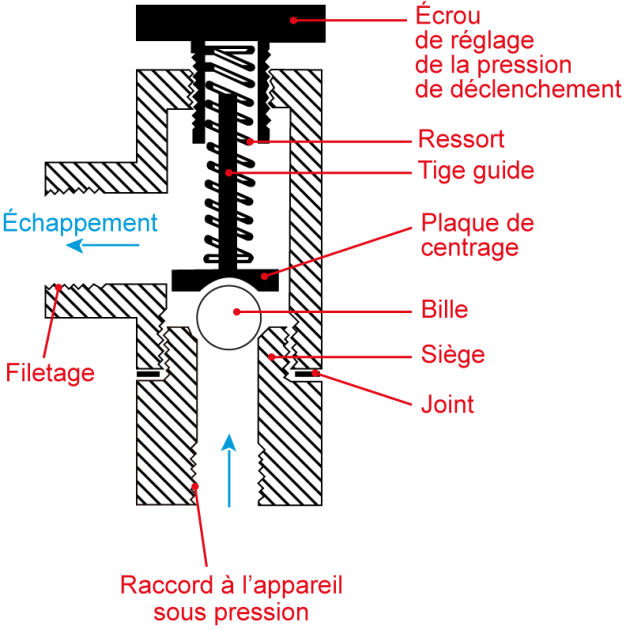
Systèmes de sécurité
Exemple :
Pour les clapets anti-retour et les soupapes de sécurité (figures ci-dessous), on peut considérer en toute première approche que \(k\approx 2,5\).
Débitmètres
Exemple :
Pour un débitmètre Venturi, \(k=0,25\cdot \left[ {{\left( \frac{D}{d} \right)}^{4}}-1 \right]\).
Pour un débitmètre à diaphragme, \(k={{\left[ 1+0,707\cdot \sqrt{1-{{\left( \frac{d}{D} \right)}^{2}}}-{{\left( \frac{d}{D} \right)}^{2}} \right]}^{2}}\cdot {{\left( \frac{D}{d} \right)}^{4}}\).