Pertes de charge dues aux variations de direction de conduite
On liste ici quelques corrélations issues de la littérature.
Coudes
Notion fondamentale :
Le passage dans un coude peut générer beaucoup de pertes de charge.
Voici deux exemples illustrés par des animations :
coude brusque
coude arrondi
Observez les animations pour comprendre comment le changement de direction génère des turbulences et donc des pertes de charge.
Corrélations
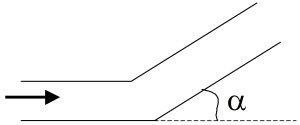
Dans le cas d'un coude brusque (c'est-à-dire à angles vifs, comme le montre la figure ci-contre), le coefficient de singularité peut alors être estimé selon : \(k=1,3\cdot \left( 1-\cos \ \alpha \right)\).
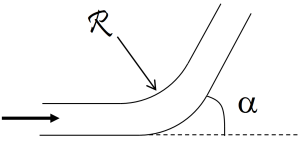
Si le coude est arrondi, on a :
\(k=\left\{ \begin{array}{r l}& \left[ 0,13+1,85\cdot {{\left( \frac{D}{2\cdot \mathcal{R}} \right)}^{3,5}} \right]\cdot \frac{\alpha}{90}\quad - \quad \rm{en\ \ r\acute{e}gime\ \ hydrauliquement\ \ lisse} \\& 0,42\cdot {{\left( \frac{D}{\mathcal{R}} \right)}^{0,5}}\quad - \quad \rm{en\ \ r\acute{e}gime\ \ hydrauliquement\ \ rugueux} \\\end{array} \right.\)
où \(\mathcal{R}\)[4] est le rayon de courbure du coude et \(\alpha\) l'angle du coude (en °).
Jonctions de conduites
Méthode :
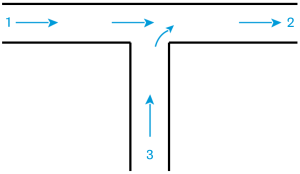
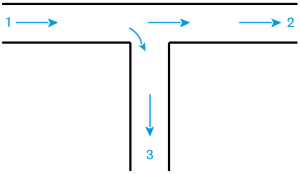
Les relations utiles pour le calcul des coefficients de singularité pour les jonctions de conduites sont données sur la figure ci-dessous.
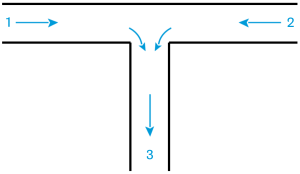
Pour une jonction à confluent symétrique, les coefficients de singularité sont :
\(k_{13} = 2 + 3 \cdot \left[ \left( \frac{Q_{v1}}{Q_{v3}} \right)^2 - \frac{Q_{v1}}{Q_{v3}} \right]\)
\(k_{23} = 2 + 3 \cdot \left[ \left( \frac{Q_{v2}}{Q_{v3}} \right)^2 - \frac{Q_{v2}}{Q_{v3}} \right]\)
avec la perte de charge à calculer selon : \(\Delta{P_{fi3}} = k_{i3} \cdot \frac{\rho \cdot u_3^2}{2}\)
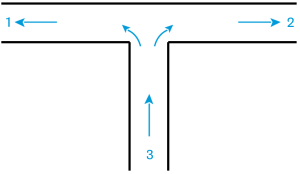
Pour une jonction à séparation symétrique, les coefficients de singularité sont :
\(k_{31} = 1 + 0,3 \cdot \left( \frac{Q_{v1}}{Q_{v3}} \right)^2\)
\(k_{32} = 1 + 0,3 \cdot \left( \frac{Q_{v2}}{Q_{v3}} \right)^2\)
avec la perte de charge à calculer selon : \(\Delta{P_{f3i}} = k_{3i} \cdot \frac{\rho \cdot u_3^2}{2}\)
Pour une jonction à confluent latéral, les coefficients de singularité sont :
\(k_{12} = 2 \cdot \frac{Q_{v3}}{Q_{v2}} - \left( \frac{Q_{v3}}{Q_{v2}} \right)^2\)
\(k_{32} = 0,6 \cdot \left[-1 + 5 \cdot \frac{Q_{v3}}{Q_{v2}} - 2 \cdot \left( \frac{Q_{v3}}{Q_{v2}} \right)^2 \right]\)
avec la perte de charge à calculer selon : \(\Delta{P_{fi2}} = k_{i2} \cdot \frac{\rho \cdot u_2^2}{2}\)
Pour une jonction à séparation latérale, les coefficients de singularité sont :
\(k_{13} = 1 + \left( \frac{Q_{v3}}{Q_{v1}} \right)^2\)
\(k_{12} = 0,4 \cdot \left( \frac{Q_{v3}}{Q_{v2}} \right)^2\)
avec la perte de charge à calculer selon : \(\Delta{P_{f1i}} = k_{1i} \cdot \frac{\rho \cdot u_1^2}{2}\)