Pertes de charge dues aux variations de section de conduite
Dans ce paragraphe, on présente les expressions du coefficient de perte de charge, en expliquant l'origine de ces pertes de charge.
Notion fondamentale : Élargissements de section
Dans le cas d'un élargissement brusque, on observe ce que l'on appelle un décollement de la veine fluide, avec développement de zones de recirculation, comme le montre l'animation suivante.
L'animation suivante montre comment ces zones de turbulence se créent.
Observez cette animation pour comprendre la problématique des pertes de charge dans les élargissements.
Ce phénomène est responsable des pertes de charge dans un élargissement brusque.
Le coefficient de singularité peut alors être calculé à partir de la relation : \(k={\left( 1-\frac{s}{S} \right)}^{2}\), où \(s\) est la section de passage de la conduite de plus faible diamètre et \(S\) celle de la conduite de plus grand diamètre.
À l'entrée dans un réservoir, on peut considérer que \(k\approx 1\).
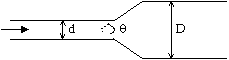
Pour limiter les pertes de charge lors d'un élargissement de section, on peut utiliser un divergent (ou diffuseur), c'est-à-dire un élargissement progressif, tel que celui de la figure ci-contre, qui "accompagne" la veine fluide. Le coefficient de singularité peut alors être estimé selon : \(k = 0,46 \cdot {{\rm{Re}}^{-0,06}} \cdot {{\left( 1-\frac{s}{S} \right)}^{0,5}}\).
On peut également utiliser l'abaque ci-dessous.
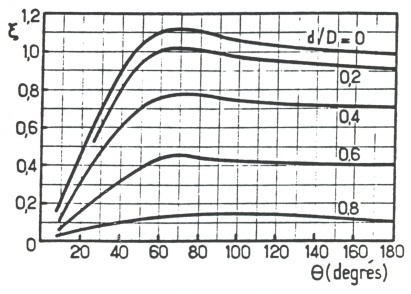
La vitesse moyenne \(\overline{u}\) utilisée pour calculer le nombre de Reynolds, ainsi que les pertes de charge singulières \(\left( \Delta {{P}_{fs}}=k\cdot \frac{\rho \cdot {{\overline{u}}^{2}}}{2} \right)\), est celle dans la conduite de plus faible diamètre, c'est-à-dire en amont.
Notion fondamentale : Rétrécissements de section
Dans le cas d'un rétrécissement brusque, on observe non seulement un décollement de la veine fluide et des zones de recirculation, mais aussi une contraction de la veine fluide au-delà du rétrécissement. Le coefficient de singularité correspondant peut être calculé à partir de la relation : \(k={{\left( \frac{1}{{{C}_{c}}}-1 \right)}^{2}}\), où \({{C}_{c}}\approx 0,59+0,41\cdot {{\left( \frac{s}{S} \right)}^{3}}\).
Comme précédemment, pour limiter les pertes de charge lors d'un rétrécissement de section, on peut utiliser un convergent, c'est-à-dire un rétrécissement progressif, tel que celui de la figure ci-contre.
Le coefficient de singularité peut alors être estimé selon :
\(k=\left\{ \begin{array}{r l}& {{\left( \frac{1}{{{C}_{c}}}-1 \right)}^{2}}\cdot \sin \ \theta \quad si\ \ \theta <90{}^\circ \\& {{\left( \frac{1}{{{C}_{c}}}-1 \right)}^{2}}\quad si\ \ \theta >90{}^\circ \\\end{array} \right.\)
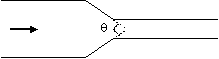
La vitesse moyenne \(\overline{u}\) utilisée pour calculer le nombre de Reynolds, ainsi que les pertes de charge singulières \(\left( \Delta {{P}_{fs}}=k\cdot \frac{\rho \cdot {{\overline{u}}^{2}}}{2} \right)\), est ici aussi celle dans la conduite de plus faible diamètre, c'est-à-dire en aval.
À la sortie dans un réservoir, on peut considérer que \(k\approx 0,5\).