Réactions exothermiques consécutives dans un réacteur piston

On met en œuvre les réactions suivantes : A →R →S en phase liquide dans un réacteur piston. Les réactions sont exothermiques à la température de travail : \(\Delta r H_1 =\) -10 kcal mol-1 & \(\Delta r H_2 =\) -20 kcal mol-1

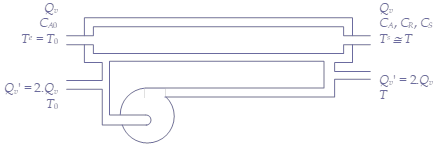
Afin de refroidir le réacteur, on fait circuler de l'eau dans une chemise extérieure. La circulation d'eau est assurée par une pompe à fort débit, de sorte que la température de l'eau dans la chemise peut être considérée comme uniforme (\(T\)). L'ensemble du circuit de refroidissement est bien isolé de l'extérieur. La boucle de refroidissement est alimentée par un débit volumique \(Q_v'\) d'eau à la température \(T_0\).

Le réacteur est alimenté par un débit volumique \(Q_v\) de solution aqueuse contenant le réactif A à la concentration \(C_{A0} =\) 5 mol L-1 ; sa température est \(T^e\). Le liquide ressort du réacteur à la température \(T^s\) et les concentrations des différentes espèces sont \(C_A^s\), \(C_R^s =\) 3,75 mol L-1 et \(C_S^s =\) 0, 75 mol L-1. Le liquide réactionnel a sensiblement les propriétés de l'eau.

L'installation a en outre les caractéristiques suivantes :

\(T_0 = T^e\) ; \(Ts \cong T\) ; \(Q_v' = 2 \cdot Q_v\)

Question

Établir le bilan thermique de cette installation. En déduire la différence de température \(T – T_0\).

Résultat

20 K

Solution

Exercice 4-2Informations[1]

Le bilan thermique de cette installation s'écrit :

\(\phi = Q_{m,caloporteur} \cdot \mathrm{Cp}_{caloporteur} \cdot \left( T_0 - T \right)\) pour le fluide caloporteur

\(\phi = Q_{m,liquide\ r\acute{e}actionnel}^e \cdot \mathrm{Cp}_{liquide\ r\acute{e}actionnel} \cdot \left( T^s - T^e \right) + F_0 \cdot X_1 \cdot \Delta r H_1 + F_0 \cdot X_2 \cdot \Delta r H_2\) pour le réacteur

Or on a : \(F_A = F_{A0} - F_0 \cdot X_1\) ; \(F_R = F_0 \cdot (X_1 - X_2)\) ; \(F_S = F_0 \cdot X_2\)

Donc \(2 \cdot Q_v \cdot \rho_{eau} \cdot \mathrm{Cp}_{eau} \cdot \left( T_0 - T \right) = Q_v \cdot \rho_{eau} \cdot \mathrm{Cp}_{eau} \cdot \left( T - T_0 \right) + \left( F_R^s + F_S^s \right) \cdot \Delta r H_1 + F_S^s \cdot \Delta r H_2\)

Soit \(3 \cdot Q_v \cdot \rho_{eau} \cdot \mathrm{Cp}_{eau} \cdot \left( T_0 - T \right) = Q_v \cdot \left( C_R^s + C_S^s \right) \cdot \Delta r H_1 + Q_v \cdot C_S^s \cdot \Delta r H_2\)

D'où \(3 \cdot \rho_{eau} \cdot \mathrm{Cp}_{eau} \cdot \left( T_0 - T \right) = \left( C_R^s + C_S^s \right) \cdot \Delta r H_1 + C_S^s \cdot \Delta r H_2\)

Ainsi \(T - T_0 = -\frac{\left( C_R^s + C_S^s \right) \cdot \Delta r H_1 + C_S^s \cdot \Delta r H_2}{3 \cdot \rho_{eau} \cdot \mathrm{Cp}_{eau}} =\)20 K

Solution en vidéo

GRC - exercice d'application : réactions exothermiques consécutives dans un réacteur piston