Bilan thermique dans un réacteur à recyclage avec échangeur extérieur
On considère le réacteur à recirculation représenté ci-dessous :
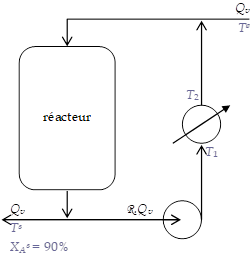
On met en œuvre une réaction exothermique (\(\Delta r H =\) - 84 kJ mol-1 à la température de travail) dans un liquide ayant sensiblement les propriétés de l'eau. Le taux de conversion du réactif est de 90% ; sa concentration en entrée de 10 000 mol m-3.
Question
Quel taux de recirculation \(\mathfrak{R}\) faut-il adopter pour que l'écart de température aux bornes de l'échangeur extérieur ne dépasse pas 10°C, sachant que l'on veut que le liquide réactionnel ressorte de l'installation à la même température que celle à laquelle il est entré ?
Solution
\(\mathfrak{R}\) doit être supérieur à 18,1
Solution
Le bilan thermique sur l'ensemble de l'installation s'écrit :
\(\phi = Q_m^e \cdot \mathrm{Cp} \cdot \left( T^s - T^e \right) + F_0 \cdot X \cdot \Delta r H (T^s) = Q_v \cdot \left[ \rho \cdot \mathrm{Cp} \cdot \left( T^s - T^e \right) + C_{A0} \cdot X_A \cdot \Delta r H \right]\)
Le bilan thermique sur l'échangeur s'écrit : \(\phi = \mathfrak{R} \cdot Q_v \cdot \rho \cdot \mathrm{Cp} \cdot \left( T_2 - T_1 \right)\)
D'où \(Q_v \cdot \left[ \rho \cdot \mathrm{Cp} \cdot \left( T^s - T^e \right) + C_{A0} \cdot X_A \cdot \Delta r H \right] = \mathfrak{R} \cdot Q_v \cdot \rho \cdot \mathrm{Cp} \cdot \left( T_2 - T_1 \right)\)
Soit \(\rho \cdot \mathrm{Cp} \cdot \left( T^s - T^e \right) + C_{A0} \cdot X_A \cdot \Delta r H = \mathfrak{R} \cdot \rho \cdot \mathrm{Cp} \cdot \left( T_2 - T_1 \right)\)
On veut \(T^s = T^e\) ; et \(T_1-T_2 <\) 10 K.
Donc \(-\frac{C_{A0} \cdot X_A \cdot \Delta r H}{\mathfrak{R} \cdot \rho \cdot \mathrm{Cp}} = T_1 - T_2 <\) 10 K \(= \Delta T_{max}\), ou encore \(\mathfrak{R} > -\frac{C_{A0} \cdot X_A \cdot \Delta r H}{\Delta T_{max} \cdot \rho \cdot \mathrm{Cp}} =\) 18,1
Solution
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.