Exercice : Fabrication du chlorure d'allyle dans un réacteur tubulaire pseudo-isotherme [GRC homogène]

Fabrication du chlorure d'allyle dans un réacteur tubulaire pseudo-isotherme

Voici un problème plus conséquent !

On désire dimensionner un réacteur tubulaire pseudo-isotherme pilote pour la fabrication du chlorure d'allyle.

Dans ce réacteur, il entre 100 mol h^-1 de propylène et 50 mol h^-1 de dichlore. Ils sont préchauffés séparément à 200°C et mélangés à l'entrée du réacteur.

Le réacteur est constitué d'un tube de diamètre 30 mm dont la paroi est maintenue à 200°C par ébullition d'éthylène glycol dans une double enveloppe. La pression de marche est constante et égale à 2 atm (pression absolue). Le coefficient de transfert entre le tube et le milieu réactionnel est \(h =\) 30 kcal h^-1 m^-2 K^-1.

La réaction principale est la suivante (Réaction 1) : Cl₂ + C₃H₆ → CH₂=CH-CH₂Cl + HCl

ou encore, en écriture simplifiée : Cl + P → A + H

Une étude préliminaire de laboratoire a montré qu'en plus de la réaction principale, une réaction annexe se produisait : une partie du dichlore se fixe par addition sur le propylène pour former du 1-2 dichloropropane (Réaction 2) : Cl₂ + C₃H₆ → CH₂Cl-CHCl-CH₃

ou encore, en écriture simplifiée : Cl + P → D

Les chaleurs de réaction ont été déterminées à 273 K et 355 K :

Réaction 1 : \(\Delta r H_1(273 K) =\) -26 800 cal mol^-1 ; \(\Delta r H_1(355 K) =\) -26 700 cal mol^-1

Réaction 2 : \(\Delta r H_2(273 K) =\) -44 000 cal mol^-1 ; \(\Delta r H_2(355 K) =\) -44 000 cal mol^-1

D'après les résultats de laboratoire, les vitesses de réaction (exprimées en moles de chlore transformées par m³ et par heure) peuvent s'écrire :

Réaction 1 : \(r_1 = k_{0,1} \cdot \exp \left( \frac{-Ea_1}{\mathbb{R} \cdot T} \right) \cdot P_P \cdot P_{Cl}\) avec \(k_{0,1} =\) 3,3 10⁹ mol m^-3 h^-1 atm^-2 et \(Ea_1 =\) 15 100 cal mol^-1

Réaction 2 : \(r_2 = k_{0,2} \cdot \exp \left( \frac{-Ea_2}{\mathbb{R} \cdot T} \right) \cdot P_P \cdot P_{Cl}\) avec \(k_{0,2} =\) 1,87 10⁵ mol m^-3 h^-1 atm^-2 et \(Ea_2 =\) 3 810 cal mol^-1

avec \(\mathbb{R} =\) 1,9865 cal mol^-1 K^-1, \(T\) étant en K et les pressions partielles en atm

Les chaleurs spécifiques des divers constituants peuvent être supposées constantes et ont les valeurs suivantes :

Propylène : \(Cp_P =\) 25,3 cal mol^-1 K^-1
Acide chlorhydrique : \(Cp_H =\) 7,2 cal mol^-1 K^-1
Chlore : \(Cp_{Cl} =\) 8,6 cal mol^-1 K^-1
Chlorure d'allyle : \(Cp_A =\) 28,0 cal mol^-1 K^-1
1-2-Dichloropropane : \(Cp_D =\) 35,1 cal mol^-1 K^-1

Question

Établir les bilans de matière et d'énergie.

PUIS :

Concevoir un fichier dans votre tableur préféré ou un programme dans votre langage favori, afin d'estimer les profils de taux de conversion et de température le long du réacteur (méthode d'EULER explicite par exemple). Tracer les courbes correspondantes et commenter la forme des profils obtenus.

Solution

Les réactions sont :

Cl + P → A + H (1)

Cl + P → D (2)

Le flux molaire d'actifs entrants est \(F_0 = F_{Cl,0} + F_{P,0}\).

Les différents flux molaires s'écrivent :
\(F_{total} = F_0 \cdot (1-X_2)\)
\(F_{Cl} = F_{Cl,0} + F_0 \cdot (- X_1 - X_2)\)
\(F_P = F_{P,0} + F_0 \cdot (- X_1 - X_2)\)
\(F_A = F_0 \cdot X_1\)
\(F_H = F_0 \cdot X_1\)
\(F_D = F_0 \cdot X_2\)

D'où : \(P_P = \frac{F_{P,0} - F_0 \cdot \left( X_1 + X_2 \right)}{F_0 \cdot \left( 1 - X_2 \right)} \cdot P\) et \(P_{Cl} = \frac{F_{Cl,0} - F_0 \cdot \left( X_1 + X_2 \right)}{F_0 \cdot \left( 1 - X_2 \right)} \cdot P\)

La variation de flux molaire de propylène due à la réaction (1) dans une tranche de réacteur piston est : \(\left. \mathrm{d}F_P \right|_1 = - r_1 \cdot \mathrm{d}V\). De même \(\left. \mathrm{d}F_P \right|_2 = - r_2 \cdot \mathrm{d}V\)

Note : en sommant les deux, on retrouve le bilan en propylène sur une tranche de réacteur piston : \(\left( - r_1 - r_2 \right) \cdot \mathrm{d}V = \mathrm{d}F_P\)

Soit \({{\left. d{{F}_{P}} \right|}_{1}}=\left[ -{{k}_{0,1}}\cdot \exp \left( \frac{-E{{a}_{1}}}{\mathbb{R} \cdot T} \right)\cdot {{P}_{P}}\cdot {{P}_{Cl}} \right]\cdot dV\), avec \(dV=\frac{\pi \cdot {{\varnothing }^{2}}}{4}\cdot dz\)

\(-{{F}_{0}}\cdot d{{X}_{1}}=-{{k}_{0,1}}\cdot \exp \left( \frac{-E{{a}_{1}}}{\mathbb{R} \cdot T} \right)\cdot \frac{\left[ {{F}_{P0}}-{{F}_{0}}\cdot \left( {{X}_{1}}+{{X}_{2}} \right) \right]\cdot \left[ {{F}_{Cl,0}}-{{F}_{0}}\cdot \left( {{X}_{1}}+{{X}_{2}} \right) \right]}{{{\left[ {{F}_{0}}\cdot \left( 1-{{X}_{2}} \right) \right]}^{2}}}\cdot {{P}^{2}}\cdot \frac{\pi \cdot {{\varnothing }^{2}}}{4}\cdot dz\)

\(\frac{d{{X}_{1}}}{dz}=\frac{\pi \cdot {{\varnothing }^{2}}\cdot {{k}_{0,1}}\cdot {{P}^{2}}}{4\cdot {{F}_{0}}}\cdot \exp \left( \frac{-E{{a}_{1}}}{\mathbb{R} \cdot T} \right)\cdot \frac{\left[ {{F}_{P0}}-{{F}_{0}}\cdot \left( {{X}_{1}}+{{X}_{2}} \right) \right]\cdot \left[ {{F}_{Cl,0}}-{{F}_{0}}\cdot \left( {{X}_{1}}+{{X}_{2}} \right) \right]}{{{\left[ {{F}_{0}}\cdot \left( 1-{{X}_{2}} \right) \right]}^{2}}}\)

De même \(\frac{d{{X}_{2}}}{dz}=\frac{\pi \cdot {{\varnothing }^{2}}\cdot {{k}_{0,2}}\cdot {{P}^{2}}}{4\cdot {{F}_{0}}}\cdot \exp \left( \frac{-E{{a}_{2}}}{\mathbb{R} \cdot T} \right)\cdot \frac{\left[ {{F}_{P0}}-{{F}_{0}}\cdot \left( {{X}_{1}}+{{X}_{2}} \right) \right]\cdot \left[ {{F}_{Cl,0}}-{{F}_{0}}\cdot \left( {{X}_{1}}+{{X}_{2}} \right) \right]}{{{\left[ {{F}_{0}}\cdot \left( 1-{{X}_{2}} \right) \right]}^{2}}}\)

Le bilan thermique sur une tranche de réacteur piston s'écrit :

\(\begin{align}& d\varphi =F\cdot Cp\cdot dT+{{F}_{0}}\cdot \left[ \Delta r{{H}_{1}}(T)\cdot d{{X}_{1}}+\Delta r{{H}_{2}}(T)\cdot d{{X}_{2}} \right] \\& =h\cdot dA\cdot \left( {{T}_{paroi}}-T \right)=h\cdot \pi \cdot \varnothing \cdot dz\cdot \left( {{T}_{paroi}}-T \right)\end{align}\)

\(F\cdot Cp\cdot \frac{dT}{dz}=h\cdot \pi \cdot \varnothing \cdot \left( {{T}_{paroi}}-T \right)-{{F}_{0}}\cdot \left[ \Delta r{{H}_{1}}(T)\cdot \frac{d{{X}_{1}}}{dz}+\Delta r{{H}_{2}}(T)\cdot \frac{d{{X}_{2}}}{dz} \right]\)

\(\begin{align}& F\cdot Cp\cdot \frac{dT}{dz}=h\cdot \pi \cdot \varnothing \cdot \left( {{T}_{paroi}}-T \right) \\& -{{F}_{0}}\cdot \left[ \begin{matrix}\frac{\pi \cdot {{\varnothing }^{2}}\cdot {{P}^{2}}}{4\cdot {{F}_{0}}}\cdot \left[ {{k}_{0,1}}\cdot \exp \left( \frac{-E{{a}_{1}}}{\mathbb{R} \cdot T} \right)\cdot \Delta r{{H}_{1}}(T)+{{k}_{0,2}}\cdot \exp \left( \frac{-E{{a}_{2}}}{\mathbb{R} \cdot T} \right)\cdot \Delta r{{H}_{2}}(T) \right] \\\cdot \frac{\left[ {{F}_{P0}}-{{F}_{0}}\cdot \left( {{X}_{1}}+{{X}_{2}} \right) \right]\cdot \left[ {{F}_{Cl,0}}-{{F}_{0}}\cdot \left( {{X}_{1}}+{{X}_{2}} \right) \right]}{{{\left[ {{F}_{0}}\cdot \left( 1-{{X}_{2}} \right) \right]}^{2}}} \\\end{matrix} \right]\end{align}\)

\(\frac{dT}{dz}=\frac{h\cdot \pi \cdot \varnothing \cdot \left( {{T}_{paroi}}-T \right)-\frac{\pi \cdot {{\varnothing }^{2}}\cdot {{P}^{2}}}{4}\cdot \left[ \begin{matrix}\left[ {{k}_{0,1}}\cdot \exp \left( \frac{-E{{a}_{1}}}{\mathbb{R} \cdot T} \right)\cdot \Delta r{{H}_{1}}(T)+{{k}_{0,2}}\cdot \exp \left( \frac{-E{{a}_{2}}}{\mathbb{R} \cdot T} \right)\cdot \Delta r{{H}_{2}}(T) \right] \\\cdot \frac{\left[ {{F}_{P0}}-{{F}_{0}}\cdot \left( {{X}_{1}}+{{X}_{2}} \right) \right]\cdot \left[ {{F}_{Cl,0}}-{{F}_{0}}\cdot \left( {{X}_{1}}+{{X}_{2}} \right) \right]}{{{\left[ {{F}_{0}}\cdot \left( 1-{{X}_{2}} \right) \right]}^{2}}} \\\end{matrix} \right]}{\left[ {{F}_{P0}}-{{F}_{0}}\cdot \left( {{X}_{1}}+{{X}_{2}} \right) \right]\cdot C{{p}_{P}}+\left[ {{F}_{Cl,0}}-{{F}_{0}}\cdot \left( {{X}_{1}}+{{X}_{2}} \right) \right]\cdot C{{p}_{Cl}}+{{F}_{0}}\cdot {{X}_{1}}\cdot C{{p}_{A}}+{{F}_{0}}\cdot {{X}_{1}}\cdot C{{p}_{H}}+{{F}_{0}}\cdot {{X}_{2}}\cdot C{{p}_{D}}}\)

NB : D'après les valeurs des chaleurs de réaction, on pourra les considérer comme constantes.

D'où le système :

\[\left\{ \begin{align}& \frac{\mathrm{d} X_1}{\mathrm{d} z} = \frac{\pi \cdot \varnothing^2 \cdot P^2}{4 \cdot F_0} \cdot k_{0,1} \cdot \exp \left( \frac{-Ea_1}{\mathbb{R} \cdot T} \right) \cdot \frac{\left[ F_{P0} - F_{0} \cdot \left( X_1+X_2 \right) \right] \cdot \left[ F_{Cl,0} - F_0 \cdot \left( X_1+X_2 \right) \right]}{\left[ F_0 \cdot \left( 1-X_2 \right) \right]^2} \\& \frac{\mathrm{d} X_2}{\mathrm{d} z} = \frac{\pi \cdot \varnothing^2 \cdot P^2}{4 \cdot F_0} \cdot k_{0,2} \cdot \exp \left( \frac{-Ea_2}{\mathbb{R} \cdot T} \right) \cdot \frac{\left[ F_{P0} - F_{0} \cdot \left( X_1+X_2 \right) \right] \cdot \left[ F_{Cl,0} - F_0 \cdot \left( X_1+X_2 \right) \right]}{\left[ F_0 \cdot \left( 1-X_2 \right) \right]^2} \\& \frac{\mathrm{d} T}{\mathrm{d} z} = \frac{h \cdot \pi \cdot \varnothing \cdot \left( T_{paroi}-T \right) -\frac{\pi \cdot \varnothing^2 \cdot P^2}{4} \cdot \left[ \left[ k_{0,1} \cdot \exp \left( \frac{-Ea_1}{\mathbb{R} \cdot T} \right) \cdot \Delta rH_1 + k_{0,2} \cdot \exp \left( \frac{-Ea_2}{\mathbb{R} \cdot T} \right) \cdot \Delta rH_2 \right] \cdot \frac{\left[ F_{P0} - F_0 \cdot \left( X_1+X_2 \right) \right] \cdot \left[ F_{Cl,0} - F_0 \cdot \left( X_1+X_2 \right) \right]}{{\left[ F_0 \cdot \left( 1-X_2 \right) \right]}^2} \right]}{\left[ F_{P0} - F_0 \cdot \left( X_1+X_2 \right) \right] \cdot Cp_P + \left[ F_{Cl,0} - F_0 \cdot \left( X_1+X_2 \right) \right] \cdot Cp_{Cl} + F_0 \cdot X_1 \cdot Cp_A + F_0 \cdot X_1 \cdot Cp_H + F_0 \cdot X_2 \cdot Cp_D} \\\end{align} \right.\]

Simulation :

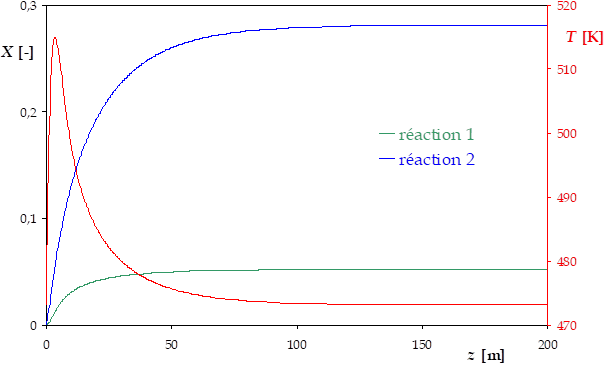
Les taux de conversion (et donc la température) n'évoluent plus que très peu au-delà de 100 m de réacteur piston. Ce réacteur est inadapté puisque le taux de conversion de la réaction parasite est nettement supérieur à celui de la réaction souhaitée. Il présente un point chaud près de l'entrée, puis est quasiment isotherme.

Solution en vidéo

GRC - exercice : fabrication du chlorure d'allyle dans un réacteur tubulaire pseudo-isotherme

Question

Comparer les profils obtenus pour différents pas d'intégration.

Solution

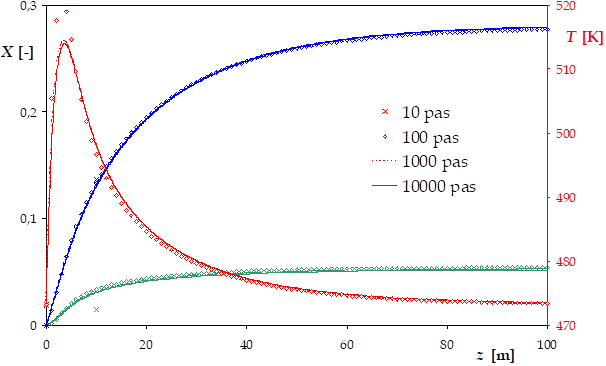
Fabrication du chlorure d'allyle dans un réacteur tubulaire pseudo-isotherme : influence du pas d'intégration | Informations^[3]

L'effet du pas d'intégration disparaît à partir d'une taille de pas intérieure à 10 cm.

Question

Recalculer les profils pour un fonctionnement adiabatique (h = 0 kcal h^-1 m^-2 K^-1) et pour un fonctionnement pseudo-isotherme (h = 500 kcal h^-1 m^-2 K^-1).

Solution

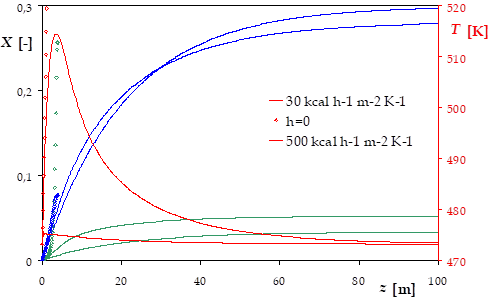
Fabrication du chlorure d'allyle dans un réacteur tubulaire pseudo-isotherme : effet de la variation du coefficient de transfert thermique | Informations^[4]

En fonctionnement adiabatique, il y a emballement dès les premiers mètres du réacteur piston.

Avec un coefficient d'échange thermique de 500 kcal h^-1 m^-2 K^-1, le profil de température est effectivement quasiment plat, on peut parler de fonctionnement pseudo-isotherme.

Question

Proposer des améliorations de fonctionnement de ce réacteur...

Solution

Faire varier la pression, la température de paroi, le rapport des débits d'alimentation, le diamètre du réacteur... afin d'obtenir un avancement de la réaction principale (1) sensiblement supérieur à celui de la réaction parasite (2), tout en préservant le caractère pseudo-isotherme du réacteur.