Applications de l'équation de BERNOULLI
Voyons à présent quelques applications classiques de l'équation de BERNOULLI.
Formule de Torricelli
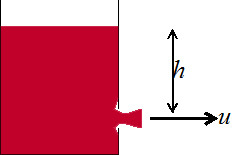
Il s'agit d'étudier l'écoulement d'un liquide à travers un orifice percé en bas d'un réservoir dont la paroi est mince (voir figure ci-contre).
Raisonnement :
La vitesse d'écoulement à travers l'orifice est donc : \(u = \sqrt{2 \cdot g \cdot h}\).
Exemple : Illustration de la formule de Torricelli

Exemple : Temps de vidange d'un réservoir
L'exercice qui suivra sur la vidange d'un réservoir permettra de mettre en application la formule de Torricelli.
Tube de Pitot
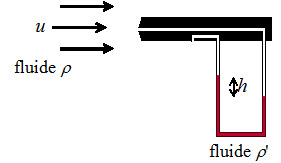
La sonde de Pitot (figure ci-contre) est un instrument de mesure de la vitesse d'un fluide.
Raisonnement :
La vitesse de l'écoulement \(u\) mesurée à l'aide du tube de Pitot est donc reliée à la différence de hauteur \(h\) dans le tube manométrique selon : \(u = \sqrt{2 \cdot \left( \frac{\rho '}{\rho}-1 \right) \cdot g \cdot h}\), \(\rho '\) étant la masse volumique du liquide manométrique et \(\rho\) celle du fluide dont on mesure la vitesse d'écoulement.
Débitmètre Venturi
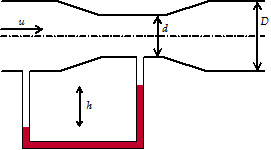
Le débitmètre Venturi repose sur la mesure de différence de pression générée par un rétrécissement de conduite comme illustré sur la figure ci-contre.
Un exercice suivant fera l'objet de la démonstration de la relation entre la différence de hauteur \(h\) dans le tube manométrique et le débit \(Q_v\) :
\(Q_v=\frac{\pi \cdot {{D}^{2}}}{4}\cdot \sqrt{\frac{2\cdot \left( \frac{\rho '}{\rho }-1 \right)\cdot g\cdot h}{{{\left( \frac{D}{d} \right)}^{4}}-1}}\)