Débitmètre Venturi
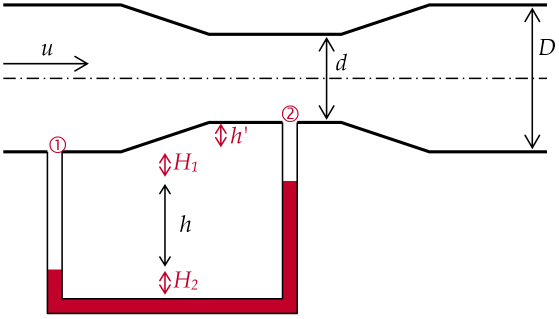
De l'eau (masse volumique \(\rho\)) circule dans la conduite schématisée ci-dessous. Le liquide manométrique a une masse volumique \(\rho' > \rho\).

Question
Donner l'expression reliant la vitesse d'écoulement à la mesure du tube manométrique et permettant de calculer le débit.
Indice
Écrivez :
l'équation de Bernoulli dans la conduite ;
le principe fondamental de l'hydrostatique dans le tube manométrique ;
la conservation de la masse dans la conduite.
Indice
En première approximation, on peut supposer que les deux prises de pression du tube manométrique sont situées à la même altitude.
Si on réalise le calcul détaillé, cette petite différence d'altitude s'annulera et on obtiendra strictement le même résultat qu'avec l'approximation.
Résultat
\({{Q}_{v}}=\frac{\pi \cdot {{D}^{2}}}{4}\cdot \sqrt{\frac{2\cdot \left( \frac{\rho '}{\rho }-1 \right)\cdot g\cdot h}{{{\left( \frac{D}{d} \right)}^{4}}-1}}\)
Solution détaillée
On écrit l'équation de BERNOULLI dans le tube Venturi entre les points 1 et 2 : \({{P}_{1}}+\rho \cdot g\cdot {{z}_{1}}+\frac{\rho \cdot {{u}_{1}}^{2}}{2}={{P}_{2}}+\rho \cdot g\cdot {{z}_{2}}+\frac{\rho \cdot {{u}_{2}}^{2}}{2}\)
On écrit la conservation de la matière :\({{Q}_{v1}}={{Q}_{v2}}\), soit \(\frac{\pi \cdot {{D}^{2}}}{4}\cdot {{u}_{1}}=\frac{\pi \cdot {{d}^{2}}}{4}\cdot {{u}_{2}}\), d'où \({{u}_{2}}={{u}_{1}}\cdot {{\left( \frac{D}{d} \right)}^{2}}\)
Enfin on écrit le principe de la hydrostatique dans le tube manométrique : \({{P}_{1}}+\rho '\cdot g\cdot {{H}_{2}}+\rho \cdot g\cdot \left( h+{{H}_{1}} \right)={{P}_{2}}+\rho '\cdot g\cdot \left( {{H}_{2}}+h \right)+\rho \cdot g\cdot \left( {{H}_{1}}+h' \right)\), d'où \({{P}_{1}}={{P}_{2}}+\left( \rho '-\rho \right)\cdot g\cdot h+\rho \cdot g\cdot h'\)
Or \({{u}_{1}}=u\) et \({{z}_{2}}-{{z}_{1}}=h'\)
Finalement, \({{P}_{2}}+\left( \rho '-\rho \right)\cdot g\cdot h+\rho \cdot g\cdot h'+\frac{\rho \cdot {{u}^{2}}}{2}={{P}_{2}}+\rho \cdot g\cdot h'+\frac{\rho \cdot {{u}^{2}}}{2}\cdot {{\left( \frac{D}{d} \right)}^{4}}\)
D'où \(\left( \rho '-\rho \right)\cdot g\cdot h=\frac{\rho \cdot {{u}^{2}}}{2}\cdot \left[ {{\left( \frac{D}{d} \right)}^{4}}-1 \right]\), soit \(u=\sqrt{\frac{2\cdot \left( \frac{\rho '}{\rho }-1 \right)\cdot g\cdot h}{{{\left( \frac{D}{d} \right)}^{4}}-1}}\).
Et \({{Q}_{v}}=\frac{\pi \cdot {{D}^{2}}}{4}\cdot \sqrt{\frac{2\cdot \left( \frac{\rho '}{\rho }-1 \right)\cdot g\cdot h}{{{\left( \frac{D}{d} \right)}^{4}}-1}}\)