Micromanomètre
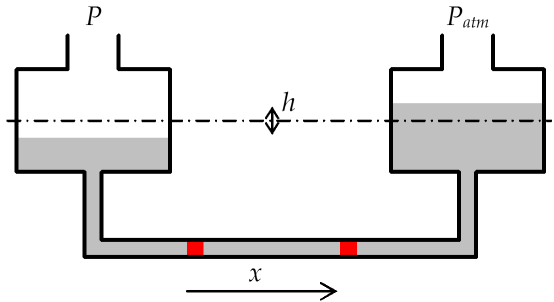
Initialement, les deux réservoirs représentés sur le schéma suivant étaient à la pression atmosphérique. Les réservoirs ont un diamètre de 2 cm, le tube inférieur a un diamètre de 0,5 mm. Ils contiennent de l'eau. On applique une pression \(P\) au réservoir de gauche (\(P-{{P}_{atm}}=\)1 Pa).
Question
De quelle distance \(x\) l'index se déplace-t-il ?
Indice
Exprimez le volume d'eau déplacée en fonction de \(h\) et en fonction de \(x\).
Indice
Attention à la définition de \(h\) sur le dessin par rapport au niveau de liquide initial (lorsque la pression appliquée est identique pour les deux réservoirs).
Résultat
8,15 cm
Solution détaillée
Le volume d'eau déplacée est \(x\cdot {{S}_{tube}}=\frac{h}{2}\cdot {{S}_{r\acute{e}servoir}}\), où \(S\) est la section.
D'où \(x=\frac{h}{2}\cdot \frac{{{S}_{r\acute{e}servoir}}}{{{S}_{tube}}}=\frac{h}{2}\cdot {{\left( \frac{{{\varnothing }_{r\acute{e}servoir}}}{{{\varnothing }_{tube}}} \right)}^{2}}\).
Pour \(P-{{P}_{atm}}=\)1 Pa, \(h=\frac{P-{{P}_{atm}}}{\rho \cdot g}=\frac{1}{1000\times 9,81}=\)1,02 10-4 m, soit 0,1 mm.
Finalement \(x=\frac{1,02\ {{10}^{-4}}}{2}\cdot {{\left( \frac{2\ {{10}^{-2}}}{0,5\ {{10}^{-3}}} \right)}^{2}}=\)0,0815 m, soit 8,15 cm.